মহাবিশ্বের মডেল বা নকশাসমূহ
এ পর্যায়ে মহাবিশ্বের একটি মডেল বিবেচনা করা যুক্তিযুক্ত হবে। মহাবিশ্বের একটি মডেল হচ্ছে একটি কল্পিত মহাবিশ্ব যা পর্যবেক্ষণযোগ্য মহাবিশ্বের সকল বস্তুকে মূর্ত করে। আর এসব পর্যবেক্ষণ থেকে কিছু যুক্তিসংগত অনুমান উদ্ভূত হবে।
বিজ্ঞান প্রকল্পে প্রায়শই ‘মডেল বা নকশা’ ব্যবহৃত হয়। ভবিষ্যদ্বাণী করার ক্ষেত্রে মডেল ব্যবহৃত হতে পারে যাকে কেউ পর্যবেক্ষণ দ্বারা বা পরীক্ষণ দ্বারা প্রমাণ করার চেষ্টা করতে পারেন। মডেল কোনও বস্তুর বা কোনও ভৌত অবস্থার ধারণাগত প্রতিমূর্তি তৈরি করতে সাহায্য করে যা থেকে বস্তুটি সম্পর্কে বোধশক্তির সৃষ্টি হয়। এদিকে মডেল বা তত্ত্বের মধ্যে স্পষ্ট কোনও পার্থক্য নেই। ‘মডেল ‘ বিষয়টি নির্মাণ কার্যের ক্ষেত্রে ব্যবহৃত হয় যা হয়ে থাকে বাস্তব কিংবা ধারণাগত। তবে সমগ্র মহাবিশ্বের ক্ষেত্রে মডেলকে হৃদয়ে ধারণ করতে হয়, বিজ্ঞানাগারের কোনও বস্তু বা কার্যপ্রণালির মডেলের মত নয়। মহাবিশ্বের বেলায় আমরা এর সামগ্রিক রূপটাকে পর্যবেক্ষণ করতে পারি না। স্যার আইজ্যাক নিউটন (১৬৪২- ১৭২৭) সামগ্রিক মহাবিশ্বের মডেল বা তত্ত্ব বিবেচনা করেছিলেন। প্রথম যারা সামগ্রিক মহাবিশ্বের মডেল বা তত্ত্ব বিবেচনা করেছিলেন তাঁদের মধ্যে তিনি একজন। তিনি স্বাভাবিকভাবেই সর্বজনীন মহাকর্ষীয় সূত্র ও গতিবিদ্যার সূত্রসমূহকে প্রয়োগ করেছিলেন। তিনি মহাবিশ্বকে সূত্রবদ্ধ করেছিলেন এবং এই মহাবিশ্বের রূপ প্রণয়ন করেছিলেন। এই সূত্রগুলো খুব সফলভাবেই গ্রহদের গতির ব্যাখ্যা দিয়েছিল। নিউটন পণ্ডিত রিচার্ড বেন্টলির কাছে একটি চিঠিতে লিখেছিলেন, ‘বস্তু যদি অসীম স্থান ব্যাপী সমভাবে বিন্যস্ত হয়ে থাকে তবে এর কিছু অংশ মিলিত হয়ে একটি সমৃদ্ধ ভরের সৃষ্টি করে থাকবে এবং আরও কিছু অংশ সৃষ্টি করে থাকবে এরকম আরেকটি ভরের। এভাবেই হয়ত সৃষ্টি হয়েছিল অসীম সংখ্যক ভরের যেগুলো পরস্পর থেকে অসীম স্থানের বুকে অতি দূর দূর বিক্ষিপ্ত ছিল। হয়ত ভরগুলো একটি স্বচ্ছ প্রকৃতি লাভ করার পর সৃষ্টি হয়েছিল স্থির সূর্য ও স্থির নক্ষত্রগুলো।’ আবার একটি সসীম অঞ্চলে বস্তু সমভাবে বিন্যস্ত হয়ে থাকলে যে মহাবিশ্ব সৃষ্টি হওয়ার কথা বিজ্ঞানী নিউটন এ ব্যাপারেও অবহিত ছিলেন। তাই তিনি উপলব্ধি করেছিলেন যে, বস্তু পুরোই তখন একটি কেন্দ্রের দিকে ঝোঁকেছিল এবং সেখানে সৃষ্টি হয়েছিল এক বিশাল গোলাকার ভর।
পরবর্তীকালে দেখা গেছে যে, সামগ্রিক মহাবিশ্বের তাত্ত্বিক কাঠামো প্রদান নিউটনের গতিবিদ্যা ও মহাকর্ষীয় সূত্রগুলো যথোপযুক্ত হয়ে ওঠেনি। নিউটন এবং তাঁর উত্তরসূরিগণ মহাজাগতিক অভিযানে পুরো সফল হতে পারেননি। তাঁরা মহাবিশ্বের সম্পর্কে একটি অনুমান তৈরি করেছিলেন যে, সমগ্র মহাবিশ্ব একটি ‘স্থির’ অবস্থায় বিরাজমান যেখানে বড়ো ধরনের কোনও পরিবর্তন হয়নি। এ ধারণা ওই সময়ে প্রকট ছিল। কিন্তু পরবর্তীকালে এ অনুমান বা ধারণা সামঞ্জস্যবিহীন হয়ে যায়। আমরা ইতোমধ্যে দেখলাম যে, মহাবিশ্ব একটি গতিশীল অবস্থায় আছে। এ ব্যাপারে পরবর্তীকালে আমরা আরও বেশি নিশ্চিত হতে পারব। অন্যদিকে, সামগ্রিক মহাবিশ্বকে বর্ণনা করতে আইনস্টাইনের আপেক্ষিকতার সাধারণ তত্ত্বটি একটি উপযুক্ত গাণিতিক ও ধারণাগত কাঠামো সরবরাহ করে। ১৯৩৪ সালে ইংরেজ জ্যোতি পদার্থবিজ্ঞানী এডওয়ার্ড আর্থার মিলনে (১৮৯৬- ১৯৫০) ডব্লিউ. এইচ. ম্যাকরের সহযোগিতায় দেখান যে, নিউটনীয় ধারণাসমূহ ব্যবহারপূর্বক আপেক্ষিক মহাজগৎ (যেমন—আইনস্টাইনের আপেক্ষিকতার সাধারণ তত্ত্বের ওপর নির্ভরশীল মহাজগৎ)-এর অনেক ফলাফল উদ্ভূত হতে পারে এই শর্তে যে, মহাবিশ্ব একটি গতিশীল অবস্থায় আছে। সুতরাং বলা যায় যে, আপেক্ষিকতার সাধারণ তত্ত্বের আবির্ভাব হওয়ার পূর্ব পর্যন্ত সৃষ্টিতত্ত্বের অগ্রগতি বিলম্বিত হওয়ার প্রয়োজন পড়েনি যদিও ‘মহাবিশ্ব স্থির’ এই ধারণাটি পরিত্যক্ত হয়েছিল। এই অনুমানটি ১৮২৬ সালে পরিত্যক্ত হয়েছিল।
জার্মান জ্যোতির্বিদ ও চিকিৎসক উইলহেম ম্যাথেউস ওলবার্স (১৭৫৭-১৮৪০) তাঁর প্যারাডক্সের একটি ভিত্তি দাঁড় করান। এক্ষেত্রে তাঁর একটি উল্লেখযোগ্য পর্যবেক্ষণ ছিল যে, রাতে আকাশ অন্ধকার দেখায়। অর্থাৎ রাতে আকাশ যে অন্ধকার দেখায় এ বিষয়টি ছিল তাঁর প্যারাডক্সের একটি ভিত্তি। তিনি দাবি করেছিলে যে, মহাবিশ্ব অসীম ও স্থির। তিনি বলেন, গড়পড়তায় দুটি নক্ষত্রের মধ্যে আপেক্ষিক বেগ লুপ্ত হয়ে যায়। তিনি এও বলেন যে, নক্ষত্রসমূহের গড় ঘনত্ব এবং পরম গড় উজ্জ্বলতা মহাকাশব্যাপী ধ্রুব। আর এক্ষেত্রে নক্ষত্র প্রদত্ত এ গড়সমূহ পর্যাপ্ত পরিমাণে বড়ো অঞ্চলে গৃহীত হয়। তিনি পরোক্ষভাবে এও দাবি করেছিলেন যে, মহাবিশ্ব ইউক্লেডিয়ান অর্থাৎ স্পেসের সর্বত্রই ইউক্লেডের জ্যামিতি চরিতার্থ। কিন্তু তিনি তাঁর এসব যুক্তিসংগত অনুমানগুলোতে অসংগতি দেখিয়েছিলেন। এই অসংগতি নিম্নরূপ : একটি গোলাকার সেল নির্বাচন করা যাক। এই শেলের কেন্দ্র হচ্ছে মহাশূন্যের কিছু সার্বভৌম বিন্দু ‘o’। শেলটির ব্যাসার্ধ ধরা যাক r এবং বেধ h। ধরা যাক, h এর তুলনায় r অনেক বৃহত্তর। সুতরাং, শেলের ভিতরের পৃষ্ঠদেশের ক্ষেত্রফল 4πr^2। এখানে : এর মান ২২/৭ , এর কাছাকাছি। শেলের আয়তন ধরা যেতে পারে 4arh এর কাছাকাছি। এখন ধরে নেওয়া যাক প্ৰতি একক আয়তনে ‘L’ পরিমাণ আলো নির্গত হয়। আর নক্ষত্রসমূহের সংখ্যা ঘনত্বকে প্রত্যেক নক্ষত্রের পরম উজ্জ্বলতা দ্বারা গুণ করে এই “ কে পাওয়া যায়। অতএব, গোলাকার শেল থেকে নির্গত আলো দাঁড়ায় 4πr^2hl। এবার উৎস থেকে নির্গত আলোর তীক্ষ্ণতা দূরত্বের বর্গের ব্যস্তানুপাতে কমতে থাকে। অর্থাৎ দূরত্ব ‘দ্বিগুণ’ হলে আলোর তীক্ষ্ণতা হয়ে যায় এক-চতুর্থাংশ। সুতরাং এই বিষয়টি থেকে বোঝা যায় যে, কেন্দ্ৰ ‘o’ তে আলোর তীক্ষ্ণতার কারণ হল গোলাকার শেলের নক্ষত্রসমূহ। আর এই তীক্ষ্ণতা দাঁড়ায় l যা বৃত্তের ব্যাসার্ধের ওপর নির্ভরশীল নয়। যদি আমরা একের পর এক সম তীক্ষ্ণ আলো-বিশিষ্ট কতগুলো শেল দ্বারা আমাদের এ শেলটি পরিবেষ্টন করি তবে প্রতিটি শেলের বাহিরের সীমারেখা পরবর্তী শেলের ভিতরের সীমারেখায় পরিণত হবে। এক্ষেত্রে শেলগুলো প্রথম শেলটির সমকেন্দ্রীয় হবে।
কেন্দ্র ‘o’ এর বিকিরণ ঘনত্বের ক্ষেত্রে প্রতিটি শেল একই রকম অবদান রাখবে। যেহেতু আমরা অনির্দিষ্টভাবে শেল যুক্ত করেছি, তাই দেখা যায় যে, কেন্দ্রে বিকিরণ ঘনত্ব অসীম হয়ে গেছে। সুতরাং, একটি নক্ষত্র হতে নির্গত আলো ০ কেন্দ্র অভিমুখে যাত্রাপথে অন্যটি দ্বারা শোষিত হতে পারে এই ব্যাপারটি আমরা এই বিশ্লেষণে উপেক্ষা করেছি। বিষয়টি বিবেচনায় নিয়ে দেখা যায় যে, o কেন্দ্রে বিকিরণ ঘনত্ব একই হওয়া উচিত যেমনটি গড় নক্ষত্রের পৃষ্ঠতলে হয়। সুতরাং, কিছু সাধারণ অনুমান থেকে এ সিদ্ধান্তে উপনীত হওয়া যায় যে, একটি নক্ষত্রের পৃষ্ঠতলের উষ্ণতার মতই আকাশপটের যে কোনও স্থানই উষ্ণ হতে পারে। এই আলোচনায় একটি অনুমান নিহিত যে, অতীতে অসীম সময়ের জন্য মহাবিশ্বকে অস্তিত্বমান হওয়ার কথা। আর বিকিরণ এ অসীম সময়ে দীর্ঘ দূরত্বসমূহ অতিক্রম করেছে এবং তাপীয় সাম্যাবস্থায় বিরাজ করেছে। অসীম সময়ের একটি স্থির অবস্থা অবশ্যই তাপজাতীয় সাম্যাবস্থায় পৌঁছেছে—এই বিষয়টি বিবেচনা করলে উপরের সিদ্ধান্তের মত একই সিদ্ধান্ত আসতে পারে। এক্ষেত্রে প্রত্যেক নক্ষত্র ঠিক যে পরিমাণ বিকিরণ নির্গত করেছে ঠিক সেই পরিমাণ বিকিরণ শোষণও করেছে।
উপরের সিদ্ধান্ত পর্যবেক্ষণবিরোধী হয় বলে এই বিশ্লেষণের অনুমানগুলোর একটি তো ভুল হবেই। এটি প্রতীয়মান যে, অনুমানগুলোর কতেক বাস্তবিকই ভুল। মহাবিশ্ব স্থির নয় এবং এটি অসীম পুরোনো নয়। ওলবার্স যে যৌক্তিকতায় ধারণা করেছিলেন অন্ততপক্ষে সে যৌক্তিকতায়ও নয়। একটি প্রসারণশীল মহাবিশ্বে দূরের গ্যালাক্সিগুলো থেকে নির্গত আলোর লোহিত সরণ ঘটে এবং শক্তি ক্ষয় হয়। ফলে আলোর তীক্ষ্ণতা দূরত্বের বর্গের ব্যস্তানুপাতে দ্রুততর কমতে থাকে যা উপরের বিশ্লেষণের বিপরীতমুখী। যদি সে সময় ওলবার্সের প্রস্তাবিত প্যারাডক্সটি গুরুত্বের সঙ্গে গৃহীত হত তাহলে মানুষ প্রশ্ন তুলত কীসের ভিত্তিতে অনুমানগুলো উদ্ভূত হয়েছিল। মহাবিশ্বের প্রসারণশীলতার ব্যাপারটি বিরাট বিস্ময়ের হয়ে ধরা দিতো না—এমনটি হয়েছিল কেবল বিজ্ঞানী হাবলের আবিষ্কারের পর
বর্তমান প্রেক্ষাপটে দাঁড়িয়ে আমি মহাবিশ্বের একটি আদর্শ মডেলকে বর্ণনা করব। এটি প্রকৃতপক্ষে কতিপয় মডেলের সংকলন। কিন্তু সব ধরনের পর্যবেক্ষণ মানানসই কোনও মডেল এখনও পর্যন্ত নেই। মহাবিশ্বের যে মডেলটি এখানে বিবেচনা করা হচ্ছে মনে হবে যেন আমি সত্যিকার মহাবিশ্ব নিয়ে আলোচনা করছি। কিন্তু বাস্তবে এটি মহাবিশ্বের একটি মডেলমাত্র। অনেক পর্যবেক্ষণ থেকে প্রাপ্ত অনুমান ও যুক্তির ওপর নির্ভর করে এই মডেলে সত্যিকার মহাবিশ্বকে ধারণ করে এর অনেক বিষয় ও বৈশিষ্ট্য বর্ণনা করব। ইতোমধ্যে কিছু সংখ্যক অনুমান ও যুক্তি তুলে ধরা হয়েছে।
আমরা যেমনটি দেখেছি যে, মহাবিশ্ব সমস্বত্বরূপে প্রতীয়মান হয়। আর আমরা যতটুকু শনাক্ত করতে পেরেছি দেখা গেছে মহাবিশ্ব ‘আইসোট্রপিক বা সমরূপীয়। এই বিষয়গুলো একটি ‘মডেল ইউনিভার্স’ সম্পর্কে ধারণা দেয় যাদেরকে বলা হয় মহাজাগতিক মূলনীতি। এই নীতি অনুসারে মহাবিশ্ব সর্বত্র সমস্বত্বরূপে বিরাজমান এবং এর প্রতিটি পয়েন্ট আইসোট্রপীয়। কিন্তু এই সমস্বত্বতা এবং সমরূপীতা গড় যুক্তিতে বিবেচনা করতে হয়। এই অনুমান খুবই গুরুত্বপূর্ণ এবং উল্লেখযোগ্য যে, মহাবিশ্বকে মনে হয় এই নীতির অনুবর্তী হবে। মহাজাগতিক এই তত্ত্ব মহাবিশ্বকে একটি একক অস্তিত্বশীল বস্তু হিসেবে বিবেচনা করতে সম্ভব করে তুলবে। এই তত্ত্ব দাবি করে যে, মহাবিশ্ব সাধারণত অনিয়মিতভাবে বিন্যস্ত গ্যালাক্সিসমূহের এলোমেলো সম্ভার নয় বরং এটি একটি একক অস্তিত্বশীল বস্তু। কিছু দৃষ্টিকোণ থেকে মহাবিশ্বের সব অংশই পরস্পরের সঙ্গে একটি ঐক্যে রয়েছে।
এই মহাজাগতিক তত্ত্ব মহাবিশ্বের বড়ো পরিসরের কাঠামোর বিবেচনা করাটাকে যথেষ্ট পরিমাণে সহজ করে দেয়। তত্ত্ব বলে, দুটি সাধারণ গ্যালাক্সির মধ্যবর্তী দূরত্বের একটি সর্বজনীন গুণক বা ফ্যাক্টর রয়েছে আর একই বিষয় যে কোনও জোড়া গ্যালাক্সির ক্ষেত্রেও। এই বিষয়টি নিম্নরূপ ধরা যাক, যে কোনও দুটি সাধারণ গ্যালাক্সি যথাক্রমে A ও B। এরা মহাবিশ্বের সম্প্রসারণের সাধারণ গতিতে অংশগ্রহণ করে চলেছে। এবার দুটি গ্যালাক্সির মধ্যবর্তী দূরত্ব পাওয়া যাবে সংখ্যা ‘fAB’ এবং ‘R’ এর মধ্যে গুণন শেষে। এখানে ‘f’ A ও B এর ওপর নির্ভরশীল। সুতরাং, এদের মধ্যবর্তী দূরত্ব দাঁড়ায় fAB। [এখনে ‘f’ মুলত ফাংশন সাইন, সেটা এখানে আমরা দিতে পারছি না, কারণ দিলে পোস্ট সেভ হয় না।]
এখানে fAB সময়ের সঙ্গে পরিবর্তিত হয়। মহাবিশ্বের ইতিহাসে বিভিন্ন কালে R-এর মান বিভিন্ন হবে কারণ R সময়ের সঙ্গে পরিবর্তিত হয়। কিন্তু fAB সময়ের সঙ্গে পরিবর্তিত হয় না। গণিত শাস্ত্রে এই বিষয়টিকে এই বলে প্রকাশ করা হয় যে, R হচ্ছে সময়ের একটি ফাংশন অর্থাৎ এটি সময় আপেক্ষিক কিন্তু fAB সময়ের ওপর নির্ভরশীল নয়। মহাজাগতিক তত্ত্বের ফলাফলগুলোর মধ্যে একটি হল-যে কোনও দুটি সাধারণ গ্যালাক্সির মধ্যবর্তী দূরত্ব একইরূপ। উদাহরণস্বরূপ, দুটি গ্যালাক্সি ‘C ও D’ যারা মহাবিশ্বের সম্প্রসারণের সঙ্গে সমতালে অংশগ্রহণ করছে। তাদের মধ্যবর্তী দূরত্ব fCDR। এক্ষেত্রে ‘fCD’ মানটি গ্যালাক্সিদ্বয়ের ওপর নির্ভরশীল এবং এই মান সময়ের সঙ্গে পরিবর্তিত হয় না। এই ফলাফলের প্রধান একটি প্রভাব হল এই যে, নির্দিষ্ট কাল শেষে গ্যালাক্সি A ও গ্যালাক্সি B এর মধ্যবর্তী দূরত্ব দ্বিগুণ হলে একইরূপে C ও D এর মধ্যবর্তী দূরত্বও দ্বিগুণ হবে। মহাবিশ্বের বড়ো পরিসরের কাঠামো ও প্রকৃতিকে একক রাশি ‘R’ দ্বারা বর্ণনা করা যেতে পারে। আর পূর্বেই উল্লেখ করা হয়েছে যে ‘R’ সময়ের সঙ্গে পরিবর্তিত হয়। মহাজাগতিক বিদ্যায় মুখ্য সমস্যাগুলোর মধ্যে একটি হচ্ছে —’R’ কীভাবে সময়ের সঙ্গে পরিবর্তিত হয় তা নির্ধারণ করা। এই R রাশিকে বলা হয়, ‘স্কেল ফ্যাক্টর (গুণনীয়ক তুলাদণ্ড)’ বা মহাবিশ্বের ব্যাসার্ধ। কিন্তু ‘R’ মহাবিশ্বের ব্যাসার্ধ—এই বিষয়টি কিয়ৎ বিভ্রান্তিকর। কারণ আমরা দেখি যে, মহাবিশ্ব স্থানের ব্যাপ্তির দিক দিয়ে সীমাহীনরূপে বৃহৎ। সুতরাং, এক্ষেত্রে তার ব্যাসার্ধ সসীম হতে পারে না। তারপরও এটি হতে পারে যে, মহাবিশ্ব স্থান বা দূরত্বের ব্যাপ্তির দিক দিয়ে সীমাবদ্ধ বা সসীম। এক্ষেত্রে R মহাবিশ্বের দুটি অবস্থান বিন্দুর মধ্যবর্তী চরম দূরত্বের সঙ্গে সম্পর্কযুক্ত। আর এই অনিশ্চয়তার কারণে R-কে আমি ‘স্কেল ফ্যাক্টর’ বলতে বেশি ইচ্ছুক।
বিজ্ঞানী হাবল সমগ্র মহাবিশ্বের গ্যালাক্সিগুলোর সরণ আবিষ্কার করেছিলেন। এবার গ্যালাক্সিদের সরণ সম্পর্কে বোঝার চেষ্টা করব। এক্ষেত্রে একটি গোলাকার বেলুনের উপমিতি বিবেচনা করাটা আশাপ্রদ হবে। ধরা যাক, বেলুনটি সম্প্রসারণশীল যেটি এর পৃষ্ঠতল জুড়ে সমভাবে আচ্ছাদিত। আর এ আচ্ছাদিত পৃষ্ঠতল জুড়ে কিছু বিন্দু বা ডট রয়েছে। দৃশ্যটি ৩.৭ নম্বর চিত্রে দেখানো হল। এখানে আমাদের উচিত বেলুনের পৃষ্ঠতলের দিকে মনোনিবেশ করা।
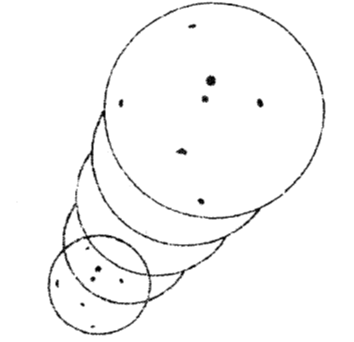
চিত্র-৩.৭ : সম্প্রসারণশীল মহাবিশ্বকে একটি সম্প্রসারণশীল বেলুনের সঙ্গে তুলনা করা হল। বেলুনটির পৃষ্ঠদেশজুড়ে অনেক বিন্দু (dot) রয়েছে। বেলুনের পৃষ্ঠদেশের যে কোনও স্থানের বিন্দুগুলো তাদের মধ্যকার পারস্পরিক দূরত্ব অনুপাতে পরস্পর থেকে একটা গতিতে দূরে সরে যাচ্ছে।
আমরা বেলুনটির পরিবেষ্টক (চতুষ্পার্শ) স্থানকে উপেক্ষিত রাখব অর্থাৎ যে স্থানে বেলুনটি অধিষ্ঠিত বা অনুবিদ্ধ আছে। আমরা ধরে নিতে পারি যে, বেলুনটিতে অনেক দ্বি-মাত্রিক দেহভৃৎ রয়েছে যারা এই পৃষ্ঠতল ত্যাগ করতে পারে না। আর এই বেলুনটি হচ্ছে তাদের সমগ্র মহাবিশ্ব। এই বিন্দুগুলোকে গ্যালাক্সির অনুরূপ বিবেচনা করা যেতে পারে। বেলুনটি প্রসারিত হওয়ার সঙ্গে সঙ্গে বিন্দুগুলোও পরস্পরের থেকে দূরে সরে যেতে থাকে। যে কোনও প্রদত্ত বিন্দু থেকে সকল বিন্দুই দূরে সরে যেতে প্রস্তুত। প্রদত্ত বিন্দু থেকে প্রদত্ত যে কোনও সময়ে অন্যসব বিন্দু বেলুনের পৃষ্ঠতল বরাবর প্রদত্ত বিন্দুটির দূরত্ব অনুপাতে একটা গতিতে দূরে সরে যেতে থাকে। এই বিষয়টি সহজেই হাবলের সূত্রানুযায়ীই প্রতিষ্ঠিত হতে পারে।
অন্যকথায় ধরা যাক, একজন পর্যবেক্ষক বিন্দুগুলোর কোনও একটিতে অবস্থান করছেন। অতঃপর ওই ব্যক্তি থেকে যে কোনও বিন্দুর সরণবেগ পাওয়া যাবে পৃষ্ঠতল বরাবর ওই বিন্দুর দূরত্বকে একটি নির্দিষ্ট সংখ্যা দিয়ে গুণ করে। যে কোনও বিন্দু বিবেচনায় সংখ্যাটি একই হবে। আর এই সংখ্যাটি হল হাবলের ধ্রুবক। সকল বিন্দুর হাবভাবও হবে একই। এমনকি প্রত্যেক বিন্দুই প্রসারণের কেন্দ্র হিসেবে বিবেচিত হতে পারে। এ থেকে বিষয়টি পরিষ্কার যে, যদিও বিন্দুগুলো পরস্পর থেকে দূরে সরে যাচ্ছে তবে এখানে কোনও নির্দিষ্ট কেন্দ্ৰীয় বিন্দু নেই অর্থাৎ এখানে বিশেষ অধিকার প্রাপ্ত কোনও বিন্দু নেই যেটি কেন্দ্রীয় বিন্দু হিসেবে বিবেচিত হতে পারে। ঠিক একইরকম পদ্ধতিতে আমাদের গ্যালাক্সি থেকে অন্যসব গ্যালাক্সি দূরে সরে যাচ্ছে। একই প্রকারে আমাদের গ্যালাক্সিরও বিশেষ কোনও অধিকারপ্রাপ্ত স্থান নেই বরং আমরা একই সরণ পর্যবেক্ষণ করব। এমনকি এটিও দেখার বিষয় না যে, আমরা কোনও গ্যালাক্সিতে অবস্থিত।
এ বেলুনের সঙ্গে মহাবিশ্বের এই সাদৃশ্যটি আরও আলোচনা করা যেতে পারে। ধরা যাক, পৃষ্ঠদেশে অবস্থিত আমাদের দুটি বিন্দু (dot) রয়েছে। বিন্দুগুলো যথাক্রমে A ও B। এবার A বিন্দু ও B বিন্দুকে সরলরেখা দ্বারা কেন্দ্রবিন্দু ‘o’ যুক্ত করা যাক যা ৩.৮ নম্বর চিত্রে দেখানো হয়েছে। এবার কোণ ∠AOB কে বলা যাক ৪AB এবং একে সমত্রিজ্যাকোণে বা রেইড়িয়ানে পরিমাপ করা যাক।
৯০° কোণকে বলা হয় এক সমকোণ যা ১/২ π রেইডিয়ানস। এখানে π-এর মান প্রায় ২২/৭ । অতঃপর এটি একটি সাধারণ জ্যামিতিক ব্যাপার যে, ধAB কে বেলুনের ব্যাসার্ধ দ্বারা গুণ করে পৃষ্ঠতল বরাবর অর্থাৎ এক বড়ো বৃত্ত বরাবর A ও B এর মধ্যবর্তী দূরত্ব পাওয়া যাবে। এখানে বড়ো বৃত্তটি এমন একটি বৃত্ত যাতে একটি সমতল পৃষ্ঠ গোলাকার পরিমণ্ডলের কেন্দ্র বরাবর ওই গোলাকার পরিমণ্ডলের পৃষ্ঠদেশকে ছেদ করে। এবার ধরা যাক ‘R’ বেলুনের ব্যাসার্ধ। যেহেতু ব্যাসার্ধ পরিবর্তনশীল, তাই বিভিন্ন সময়ে R -এর মান বিভিন্ন হবে। অতএব, পৃষ্ঠদেশ বরাবর A ও B বিন্দু দুটির মধ্যবর্তী দূরত্ব দাঁড়ায় θABR ́। এখন বেলুনটি প্রসারিত হলেও θAB স্থির, যেহেতু বিন্দুদ্বয় A ও B এর ওপর নির্ভরশীল। যেহেতু পৃষ্ঠদেশ সমভাবে প্রসারিত হয়, তাই প্রদত্ত যে কোনও দুটি বিন্দু দ্বারা ওই কেন্দ্র সম্মুখে গঠিত কোণও একই থাকে।
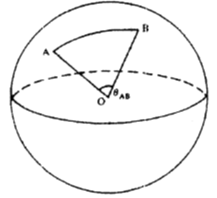
চিত্র-৩. ৮ : রেখাচিত্রটি গোলাকার বৃত্তের ওপর দুটি বিন্দুর মধ্যবর্তী দূরত্বকে চিত্রিত করে। কেন্দ্র o তে দুটি বিন্দুকে যুক্ত করলে কেন্দ্রসম্মুখে একটি কোণ উৎপন্ন হয়।
পৃষ্ঠতল বরাবর যে কোনও দুটি বিন্দুর মধ্যবর্তী দূরত্বও একইরূপ হবে। উদাহরণস্বরূপ, θCDR ́ যেখানে বিন্দু C ও বিন্দু D দ্বারা কেন্দ্রসম্মুখে θCD কোণ তৈরি করে এবং θCD সময়ের সঙ্গে পরিবর্তিত হয় না। পাঠক লক্ষ করে থাকবেন যে, পূর্বে দুটি বিন্দুর মধ্যবর্তী দূরত্বের রূপ ও দুটি গ্যালাক্সির মধ্যবর্তী দূরত্বের রূপের মধ্যে সাদৃশ্য দেখানো হয়েছিল। এখানে বিন্দুগুলোর সরণবেগ দেখাতে এই আলোচনাকে একটু প্রসারিত করা যেতে পারে। বিন্দুগুলোর সরণবেগ তাদের দূরত্বের আনুপাতিক ঠিক গ্যালাক্সিদের জন্য হাবলের সূত্রের মত। গ্যালাক্সিদের জন্য হাবল যে সূত্র প্রয়োগ করেছিলেন তা গড়পড়তায় সত্য, কিন্তু এখানে বেলুনের বিন্দুগুলোর সঙ্গে দেখানো সম্পর্কগুলো যথাযথভাবে সত্য। দুটি বিন্দুর মধ্যবর্তী দূরত্ব থেকে এও দেখা যায় যে, যদি একটি নির্দিষ্ট সময়কালে সাধারণ দুটি বিন্দু যথাক্রমে A ও B এর মধ্যবর্তী দূরত্ব দ্বিগুণ হয়, তবে অন্য যে কোনও দুটি সাধারণ বিন্দুর মধ্যবর্তী দূরত্বও দ্বিগুণ হয় একই পর্যায়কালে।
অবশ্যই কিছু ক্ষেত্রে এই সম্প্রসারমাণ বেলুনটির উদাহরণ মহাবিশ্ব থেকে খানিকটা ভিন্ন। উদাহরণস্বরূপ, যে কোনও প্রদত্ত সময়ে বেলুনের বিন্দুগুলো দ্বি- মাত্রিক পৃষ্ঠতলে রয়েছে। অন্যদিকে গ্যালাক্সিগুলো বিস্তৃত হচ্ছে ত্রি-মাত্রিক স্পেসে। এমনকি স্থান প্রসারণে দিক দিয়ে বিশ্ব বেলুনের মত নয়-এটি অসীম হতে পারে। কিন্তু মহাবিশ্ব আবার স্থান প্রসারণের দিকে সসীমও হতে পারে। স্থানের ব্যপ্তির দিক দিয়ে মহাবিশ্ব অসীম না সসীম তা বর্তমানে আমাদের জানা নেই। যদি মহাবিশ্ব সীমাবদ্ধই হয় তবে এটি এমন নয় যেন গ্যালাক্সিগুলো মহাশূন্যের একটি নির্দিষ্ট বেষ্টনী পর্যন্ত অবস্থান করছে যার বাহিরে রয়েছে ফাঁকা বা শূন্য স্পেস। পক্ষান্তরে একটি সসীম মহাবিশ্বের ক্ষেত্রে এটাই দৃঢ় সত্য যে, গ্যালাক্সিগুলো সমভাবে সমগ্ৰ শূন্যস্থান ব্যাপী বিস্তৃত, কিন্তু স্থান স্বয়ং নিজের ওপরই সমাপ্ত হয়। যাতে একটি ‘সরলরেখা’ অঙ্কন করলে দেখা যাবে রেখাটি বিপরীত প্রান্ত হতে অবশেষে একই বিন্দুতে ফিরে আসবে। এই সরলরেখা বরাবর মোট দূরত্বকে মহাবিশ্বের পরিসীমা বলা যেতে পারে যেটি আবার সীমাবদ্ধ। কিছু দণ্ড যুক্ত করে দূরত্ব সমূহকে উপস্থাপন করে গবেষণাগারে আমরা মহাবিশ্বের মডেল তৈরি করতে পারি না। কারণ বিজ্ঞানাগারের এ বিষয়টি নেহাত ইউক্লেডের জ্যামিতিকে চরিতার্থ করে। মহাবিশ্বের মাপকাঠিতে (সীমাবদ্ধ মহাবিশ্বের ক্ষেত্রে) এই জ্যামিতি ইউক্লেডের জ্যামিতিকে সমর্থন করে না। সুতরাং, মহাশূন্যের নন-ইউক্লেডিয়ান প্রকৃতির একটি উদাহরণ দেওয়া হবে। আমি উপরে ‘সরল (straight)’ শব্দটি উদ্ধৃতি চিহ্ন দিয়ে উল্লেখ করেছি। কারণ একটি নন-ইউক্লেডিয়ান স্পেসে সরলরেখার কাছাকাছি বিষয়টি হচ্ছে জিওডেসিক (বক্রপৃষ্ঠের ওপর সম্ভাব্য রেখা)। সসীম মহাবিশ্বে এই রেখাগুলো জিওডেসিক পদ্ধতি অনুসরণ করে যাতে করে আমরা রেখার বিপরীত প্রান্ত থেকে একই বিন্দুতে ফিরে আসি। উদাহরণস্বরূপ, একটি গোলাকার বস্তুর পৃষ্ঠতলে জিওডেসিকগুলো হচ্ছে বড়ো বড়ো বৃত্ত। আমরা এরকম পৃষ্ঠতলে সরলরেখা অঙ্কন করতে পারি না। সুতরাং, একটি সসীম মহাবিশ্বের পরিবেষ্টন নেই। অবশ্যই অসীম মহাবিশ্বের ক্ষেত্রেও না। এই দিক বিবেচনায় এটি গোলাকার বস্তুর পৃষ্ঠতলের অনুরূপ যেটি দুই মাত্রায় সসীম কিন্তু অবাধ অর্থাৎ এর পরিবেষ্টন নেই। একটি সসীম মহাবিশ্বের বস্তুর পরিমাণও সসীম। পক্ষান্তরে মহাবিশ্ব যদি অসীম হয় তবে অসীম স্থানজুড়ে আমাদের অসীম পরিমাণ বস্তু রয়েছে। বিষয়টি তত্ত্বীয় দিক থেকে সম্ভব। কোনও সম্ভাবনাকেই হৃদয়ঙ্গম করা সম্ভব নয় এমনকি বিশেষজ্ঞদের ক্ষেত্রেও নয়, কিন্তু আপেক্ষিকতার সাধারণ তত্ত্বের কাঠামোসমেত গাণিতিকভাবে মহাবিশ্বের এসব সম্ভাবনার উপস্থাপন করা যেতে পারে। এই গাণিতিক কাঠামো এ সম্ভাবনাগুলোর একটি ধারণাগত ছবি তৈরি করতে সাহায্য করে। অবশ্যই চূড়ান্ত পরীক্ষার বিষয় হচ্ছে—যেসব পর্যবেক্ষণ অবশ্য মেনে নেওয়া হবে তাদের থেকে প্রাপ্ত ভৌত ফলাফল অনুযায়ী মডেলগুলো সঠিক কি-না? বর্তমানে সসীম ও অসীম উভয মহাবিশ্বের মডেলই যুক্তিসিদ্ধ কারণ পর্যবেক্ষণগুলো তাদের মাঝামাঝি কোনও সিদ্ধান্ত নিতে পারে না।
গ্যালাক্সিগুলো যে হারে পরস্পর থেকে দূরে সরে যাচ্ছে তা থেকে অনুমান করা যায়—অতীতে একই সময়ে তারা পরস্পরের কাছাকাছি ছিল। ওই বেলুনের উপমিতিটি আবার বিবেচনা করা যাক। বেলুনটির সম্প্রসারণের হার থেকে এটির পূর্বেরকার সম্প্রসারণ শনাক্ত করা যেতে পারে। এ থেকে অনুমান করা যাবে যে, বেলুনটি অবশ্যই একটা সময় শূন্য ব্যাসার্ধ ‘R’ নিয়ে যাত্রা শুরু করেছিল। প্রারম্ভে একই সময়ে এর সকল বিন্দু একটি ওপরটির উপড়ে গাদাগাদি করে অবস্থান করছিল। একইভাবে, যখন ‘স্কেল ফ্যাক্টর R’ শূন্যতে ছিল তখন সব গ্যালাক্সিও একটির ওপর আরেকটি গাদাগাদি করে অবস্থান করছিল। এটি বিশ্বাস করা হয় যে, প্রথম দিকে অর্থাৎ প্রায় ১০ থেকে ২০ বিলিয়ন বছর পূর্বে একটি সর্বজনীন বিস্ফোরণ ঘটেছিল। ফলে বস্তুগুলো প্রচণ্ডভাবে পরস্পর থেকে বিচ্ছিন্ন হয়ে পড়েছিল।
এ মহাবিস্ফোরণই ‘বিগ ব্যাং’ নামে পরিচিত। মহাবিশ্বের প্রতিটি পয়েন্টে এই বিস্ফোরণ ঘটেছিল। এই দিক বিবেচনায় এটি ছিল এক অস্বাভাবিক বিস্ফোরণ। অবশ্যই এর অর্থ হতে পারে যে, অসীম মহাবিশ্বের বা সসীম মহাবিশ্বের প্রতিটি পয়েন্টে এ মহাবিস্ফোরণ ঘটেছিল যেমনটি পূর্বেই উল্লেখ করা হয়েছিল। যদি মহাবিশ্ব সসীম হয় তবে এটি শুরু হয়ে থাকবে শূন্য (জিরো) আয়তন থেকে। কিন্তু অবশ্যই এটা মনে করা যাবে না যে, এক্ষেত্রে বস্তু অন্য কোনও শূন্যস্থানে ছোট্ট আয়তনে ঘনীভূত ছিল এবং বস্তু বিস্ফোরিত হয়ে চারপাশে ফাঁকা স্থানে ছড়িয়ে পড়েছিল। মূলত সসীম মহাবিশ্বে ভিতরস্থ বা বহিস্থ বলতে কিছু নেই। এক্ষেত্রে পুরো স্পেসই সসীম। আবার এটি হৃদয়ঙ্গম করাও সহজ হবে না, তবে গাণিতিক মডেলগুলো একটি ধারণাগত ছবি তৈরিতে সাহায্য করে। আমরা যে বৈশিষ্ট্যগুলো আলোচনা করে আসছি মডেলগুলো তার মানে বোঝাতে পারে। একটি অসীম মহাবিশ্ব প্রাথমিক অবস্থা থেকে শুরু করে সব সময় অসীম। যেমনই সসীম বা সীমাবদ্ধ মহাবিশ্বের ক্ষেত্রে বস্তু অধিক থেকে অধিকতর ঘন ও উষ্ণ হয়-এ বিষয়টি মহাবিশ্বের প্রাথমিক মুহূর্তের দশাকে নির্দেশ করে যাকে সাধারণত ‘স্থান-কাল অদ্বৈতবিন্দু’ বা ‘অদ্বৈতবিন্দু’ বলা হয়। প্রাথমিক ‘অদ্বৈতবিন্দু বা অদ্বৈতস্থান’ অথবা ‘বিগ ব্যাং’ এর সঠিক রূপ সম্পর্কে আমরা খুব কমই জানি। প্রাথমিক বিস্ফোরণের দরুন মহাবিশ্ব সম্প্রসারিত হচ্ছে অর্থাৎ গ্যালাক্সিগুলো পরস্পর থেকে দূরে সরে যাচ্ছে। গ্যালাক্সিদের পরস্পর থেকে পৃথক হওয়ার পেছনে কোনও বল চালিত নেই, তাদের এই গতি কেবল প্রাথমিক অভিঘাতের রেশ। মূলত মহাবিশ্বের বিভিন্ন অংশের মধ্যে মধ্যাকর্ষণের দরুন এই সরণ ধীর হয়ে আসছে।
এখন প্রশ্ন হল— ‘বিগ ব্যাং’-এর কী প্রত্যক্ষ প্রমাণ আছে? এখানে এক চিলতে প্রমাণ হল গ্যালাক্সিদের সরণ তার মানে দাঁড়ায় অতীতে মহাবিশ্বে সমস্ত বস্তু অবশ্যই খুবই সংকুচিত অবস্থায় ছিল। এখানে তথাকথিত ‘মহাজাগতিক পটভূমি বিকিরণ’ বিষয়টি আসে যার অস্তিত্ব নিম্নে আলোচনা করা হচ্ছে। আমরা যদি অতীত মহাবিশ্বের ইতিহাস খোঁজ করি, তাহলে দেখব যে তখন বস্তুগুলো অধিকতর ঘন অবস্থায় রয়েছে। অতীতে কিছু কিছু ক্ষেত্রে গ্যালাক্সিদের পৃথক অস্তিত্ব থাকতে পারে না। অবশ্যই এরা একটি অবিচ্ছিন্ন পিণ্ড হিসেবে একত্রে ছিল। এক্ষেত্রে বস্তু সংকোচিত বলে এর তাপমাত্রা বেড়ে চলে। সুতরাং, অতীতে মহাবিশ্বে বস্তু অবশ্যই তখন উচ্চ তাপমাত্রায় ছিল। মূলত এখানে এই বিশ্বাসের কারণ হিসেবে আমরা পরবর্তীকালে দেখব যে, বস্তুর অনেক তড়িৎ চুম্বকীয় বিকিরণও রয়েছে, যেমন বেতার তরঙ্গ বা রেডিও তরঙ্গ, অবলোহিত তরঙ্গ এবং আলো ইত্যাদি। কিছু পর্যায়ে এই বিকিরণ বস্তুর সাম্যাবস্থায় রয়েছে। অর্থাৎ বস্তু প্রত্যেক তরঙ্গদৈর্ঘ্যে সমপরিমাণ বিকিরণ নির্গমন ও শোষণ করে। তারপর বিকিরণ বর্ণালি একটি বিশেষ রূপ লাভ করে যা কেবল বস্তুর তাপমাত্রার ওপর নির্ভর করে তার প্রকৃতির ওপর নয়। এই বর্ণালি কিছুটা ৩.৫ নম্বর চিত্রে প্রদর্শিত লেখচিত্রের মত। এই বর্ণালিকে ‘কৃষ্ণ বস্তুর বিকিরণ’ বলে উল্লেখ করা হয়। কারণ এই বিকিরণ কৃষ্ণ বস্তু থেকে নির্গত বিকিরণের সঙ্গে সাদৃশ্যতা দেখায়। কৃষ্ণ বস্তু হচ্ছে একটি পূর্ণশোষী উত্তপ্ত বস্তু যার বিকিরণ স্বয়ং এই বস্তুর সঙ্গে তাপীয় সাম্যাবস্থায় থাকে অর্থাৎ বস্তুটি যে কোনও তরঙ্গদৈর্ঘ্যে সমপরিমাণ শক্তি শোষণ ও বিকিরণ করে। কৃষ্ণবস্তুর বিকিরণ বর্ণালির আবিষ্কার ঐতিহাসিকভাবে গুরুত্বপূর্ণ কারণ এই আবিষ্কার কোয়ান্টাম তত্ত্বের উত্থান ঘটায়। এই আবিষ্কার একটি বিষয় উদ্ঘাটন করে যে, এক প্রকার বিকিরণ শক্তির স্বতন্ত্র খণ্ডে খণ্ডে বেরিয়ে আসে পরবর্তীকালে যার নাম দেওয়া হয়েছিল ফোটন। জার্মান পদার্থবিদ ম্যাক্স কার্ল আর্নস্ট লুদভিগ প্ল্যাঙ্ক (১৮৫৮-১৯৪৭) শতাব্দীর শুরুর দিকে বিষয়টির সমাধান করেছিলেন। প্ল্যাঙ্কের ফরমুলা নিম্নরূপে (পরিমাণজ্ঞাপক) বর্ণনা করা যেতে পারে : একটি বাক্স ভরতি কৃষ্ণ বস্তুর বিকিরণ নেওয়া হল। যে কোনও তরঙ্গদৈর্ঘ্যে এই বিকিরণের শক্তি বা তীক্ষ্ণতা ক্রমবর্ধমান তরঙ্গদৈর্ঘ্যের সঙ্গে খুব খাড়াভাবে উপরে ওঠে এবং চূড়ান্ত অবস্থায় পৌঁছার পর আবার খাড়াভাবে নেমে যায়। প্রাথমিক মহাবিশ্বের চলমান দৃশ্য অনুযায়ী প্রাথমিক সময়গুলোতে বিকিরণের অবশিষ্টাংশ উচ্চ তাপমাত্রায় বস্তুর সঙ্গে সাম্যাবস্থায় থাকা উচিত। কিন্তু বর্তমানে এই বিকিরণ অধিকতর কম তাপমাত্রায় থাকা স্বাভাবিক যেহেতু মহাবিশ্বের সম্প্রসারণ বিকিরণকে শীতল করে দেয়। বর্তমানে কৃষ্ণ বস্তুর বর্ণালিসহ তড়িৎ চুম্বকীয় বিকিরণ সমগ্র মহাবিশ্ব জুড়ে পরিব্যাপ্ত হওয়া উচিত। আর এ বিকিরণের তাপমাত্রা হবে এক নির্দিষ্ট নিম্নতাপমাত্রার। এমনকি এ বিকিরণ হওয়া উচিত সমস্বত্বীয় এবং আইসোট্রপিক ঠিক মহাবিশ্ব স্বয়ং যেমন। ১৯৬৫ সালে প্রথম পদার্থবিজ্ঞানী আর. এলান পেনজিয়াস এবং জ্যোতির্বিজ্ঞানী আর. ডব্লিউ উইলসন যৌথভাবে এই ধরনের আইসোট্রপীয় বিকিরণ আবিষ্কার করেছিলেন। এ বিকিরণের তাপমাত্রা ৩ কেলভিনের কাছাকাছি। এখানে কেলভিন হচ্ছে পরমতাপমাত্রা পরিমাপের স্কেল অর্থাৎ তাপমাত্রা পরমশূন্য থেকে ঊর্ধ্বগামী হয় যা প্রায় ২৭৩° সেন্টিগ্রেডের কাছাকাছি। কেলভিনকে সংক্ষেপে K দ্বারা প্রকাশ করা হয়। পেনজিয়াস ও উইলসন এই বিকিরণকে ৭.৩৫ সেন্টিমিটার তরঙ্গদৈর্ঘ্যে পেয়েছিলেন। বিভিন্ন পর্যবেক্ষক বিভিন্ন তরঙ্গদৈর্ঘ্যে কাজ করে দেখেছেন যে, পেনজিয়াস ও উইলসনের আবিষ্কার এখনও পর্যন্ত সঠিক। যতদূর এই আইসোট্রপিক পট-বিকিরণকে প্রত্যাশিত কৃষ্ণ-বস্তুর বিকিরণ বলে ধরা হয়। অবশ্য এ বিষয়টি দৃঢ়ভাবে প্রতিষ্ঠিত হতে আরও অধিক ফলাফলের প্রয়োজন। এখানে বিকিরণকে ‘পট বা পটভূমি’ বিকিরণ বলার কারণ এই বিকিরণ বিশেষ কোথাও থেকে এসে সমগ্র মহাবিশ্ব জুড়ে ব্যাপ্ত হয়। বিকিরণ বর্ণালির তরঙ্গদৈর্ঘ্যের শীর্ষবিন্দু ০.১ λo যা ৩.৫ নম্বর চিত্রে দেখানো হল)। ০.১ সেন্টিমিটারের নিচের তরঙ্গদৈর্ঘ্যের (অবলোহিত মাত্রায়) পরিমাপ পাওয়া বায়ুমণ্ডলে খুবই কঠিন। এই ধরনের বিকিরণের ক্ষেত্রে বায়ুমণ্ডল খুবই অস্বচ্ছ। এই ধরনের পর্যবেক্ষণ বায়ুমণ্ডলের ওপরে স্যাটেলাইটে করা সম্ভব। অনেক ইঙ্গিত রয়েছে যে, ৩.৫ নম্বর চিত্রে তরঙ্গদৈর্ঘ্যের লেখচিত্রটিতে বক্ররেখা এমনইভাবে আছে যেমনটা হওয়া উচিত। অন্যান্য উৎসের ক্ষেত্রে ‘মহাজাগতিক’ পটভূমি বিকিরণ ব্যাখ্যার কিছু প্রচেষ্টা হয়েছে। অর্থাৎ মহাবিশ্বের প্রাথমিক ধাপের অবশিষ্টাংশ হিসেবে নয় এ বিকিরণের অন্য কোনও উৎস রয়েছে। উদাহরণস্বরূপ সমগ্র মহাবিশ্বব্যাপী গ্যালাক্সিগুলোর বিকিরণের দরুন এই মহাজাগতিক পটভূমি বিকিরণ তৈরি হয়। কিন্তু, এই ধরনের ব্যাখ্যাগুলো খুব সফল হয়নি।
মহাজাগতিক পটভূমি বিকিরণে একটি ন্যূনতম নিয়মাবদ্ধ ‘অ্যানিসট্রোপি’ প্রত্যাশিত। কারণস্বরূপ, যেহেতু পৃথিবী বিকিরণের মাধ্যমে পরিভ্রমণ করে সেহেতু পৃথিবী যে অভিমুখে ভ্রমণ করছে সে গতিপথ খুব সামান্য মাত্রায় উষ্ণ হওয়া স্বাভাবিক। আর পৃথিবীর ভ্রমণের সময় বিপরীতমুখ একইমাত্রায় শীতলতর হবে।
মূলত আইসোট্রপিতে এ রকম একটি নিয়মাবদ্ধ পরিবর্তন আর. এ মোলার ও তাঁর সহযোগীগণ ১৯৭৭ সালে আবিষ্কার করেছিলেন। তাঁরা দেখতে পান যে, লিও (সিংহ) নক্ষত্রমণ্ডলের অভিমুখে তাপমাত্রা ধীরে ধীরে বেড়ে চলেছে এবং এর বিপরীত অভিমুখে একই হারে শীতল হচ্ছে। এ বিষয়টি মহাবিশ্বের মধ্য দিয়ে পৃথিবীর পরম গতিকে নির্দেশ করে। বিষয়টি এও নির্দেশ করে যে, পৃথিবী প্রায় ৪০০ কিলোমিটার সেকেন্ড^-১ বেগে লিও নক্ষত্রমণ্ডলের দিকে সরে যাচ্ছে। প্রকৃতপক্ষে, পৃথিবী সূর্যের চারদিকে ঘুরছে আর সূর্য গ্যালাক্সির কেন্দ্রের চারপাশে ঘুরছে। কেউ এইসব গতিকে যখন একত্রে আমলে নেন তখন এই সিদ্ধান্তে পৌঁছেন যে, আমাদের গ্যালাক্সি মহাশূন্যের মধ্য দিয়ে প্রায় ৬০০ কিলোমিটার সেকেন্ড^-১ বেগে চলছে। এই বেগ বরং বিশাল কিন্তু ব্যাখ্যার ঊর্ধ্বে নয়। উদাহরণস্বরূপ, এটি সৃষ্টি হচ্ছে গ্যালাক্সিদের স্থানীয় স্তবকের চারপাশে আমাদের গ্যালাক্সির পরিক্রমণের দরুন।
মহাজাগতিক বিদ্যায় বা সৃষ্টিতত্ত্বে সবচেয়ে গুরুত্বপূর্ণ দুটি পর্যবেক্ষণের মধ্যে একটি হচ্ছে মহাজাগতিক পটভূমি বিকিরণ। আর অন্যটি হল বিজ্ঞানী হাবলের আবিষ্কার — ‘গ্যালাক্সিদের সরণ’। মহাজাগতিক পটভূমি বিকিরণের অস্তিত্ব একটি জোরালো ইঙ্গিত দেয় যে, প্রাথমিক পর্যায়ে মহাবিশ্ব একটি উষ্ণ ও ঘনীভূত অবস্থা অতিক্রম করে এসেছিল। বস্তু ও বিকিরণ তখন সাম্যাবস্থায় ছিল। আর এই প্রমাণ ‘বিগ ব্যাং’কে সমর্থন করে। এই বিগ ব্যাং-কেই বলা হয় মহাবিশ্বের উৎস। যা হোক, মহাবিশ্বের উৎস সম্পর্কিত জটিল সমস্যার সমাধান হয়েছে—একথা বলা অকালপক্কতাই হবে। বিগ ব্যাং-এর সঠিক প্রকৃতি জানতে এখনও পর্যন্ত অনেক কিছুই বাকি রয়েছে। বিশেষ করে এখানে আরও প্রশ্নের জন্ম হয়— ‘বিগ ব্যাং’-এর পূর্বেও কী মহাবিশ্বের অন্য কোনও পর্যায় ছিল বা বিগ ব্যাং-এর মুহূর্তে কি সময়ের গোড়াপত্তন হয়েছিল। এসব বিষয় বিজ্ঞানের সবচেয়ে কঠিন প্রশ্ন যেগুলোর সন্তুষ্টিজনক কোনও উত্তর এখনও পর্যন্ত নেই।
