১০. ভর ভরবেগ শক্তি এবং ক্রিয়া

১০. ভর ভরবেগ শক্তি এবং ক্রিয়া

পরিমাণগত নির্ভুলতার চেষ্টা যেমন কষ্টসাধ্য তেমনি গুরুত্বপূর্ণ। ভৌত মাপন করা হয় অসাধারণ নির্ভুলতার সঙ্গে। মাপন ক্রিয়ায় কম যত্ন নেওয়া হলে যে সূক্ষ্ম ভুলগুলি অপেক্ষবাদের পরীক্ষামূলক উপাত্ত সেগুলি কখনোই প্রকাশিত হতো না। অপেক্ষবাদের আগে গাণিতিক পদার্থবিদ্যা যে কল্পনগুলি ব্যবহার করত সেগুলিকে মনে করা হতো ভৌত মাপনের মতোই নির্ভুল কিন্তু পরে দেখা গেল সেগুলি যৌক্তিক দোষদুষ্ট। এই দোষ প্রকাশ পেয়েছে গণনার ভিত্তিতে যা আশা করা গিয়েছিল তা থেকে সামান্য বিচ্যুতিতে। এই অধ্যায়ে আমি দেখাতে চাই অপেক্ষবাদের আগেকার ভিতরে কি পরিবর্তন আনতে হয়েছে।

ভর সম্পর্কে এর আগে আমরা বলেছি। আমাদের দৈনন্দিন জীবনযাত্রার ক্ষেত্রে ভর এবং ওজন একই। আউন্স, গ্রাম ইত্যাদি ওজন করার সাধারণ বাটখারাগুলি আসলে ভরের মাপ। কিন্তু নির্ভুল মাপন শুরু করার সঙ্গে সঙ্গেই আমরা ভর এবং ওজনের পার্থক্য মানতে বাধ্য হই। ওজন করার দুটি পদ্ধতি সাধারণত ব্যবহার করা হয় দাঁড়িপাল্লা আর স্প্রিং-এর ওজনকল। ভ্রমণে যাওয়ার সময় আপনার মালপত্র চাপানো হয় স্প্রিং-এর উপরে, দাঁড়িপাল্লায় নয়। ওজনের চাপে স্প্রিং খানিকটা নেমে যায় আর সেটা দেখানো হয় ডায়ালের (dial- মুখপট্ট) উঁচ দিয়ে। আপনার ওজন দেখাবার জন্য যে স্বয়ংক্রিয় যন্ত্র আছে তাতেও একই পদ্ধতি ব্যবহার করা হয়। স্প্রিং-এর ওজনকল দেখায় ওজন কিন্তু দাঁড়িপাল্লা দেখায় ভর। যতক্ষণ আপনি পৃথিবীর একই অংশে রয়েছেন ততক্ষণ এ পার্থক্যে কিছু এসে যায় না। কিন্তু আপনি যদি বিভিন্ন স্থানে দুই ধরনের দুটি ওজনকল ব্যবহার করেন এবং সেগুলি যদি নির্ভুল হয় তাহলে দেখবেন তাদের মাপনফল সব সময় এক হয় না। দাঁড়িপাল্লার মাপনফল সব জায়গায়ই এক হবে কিন্তু স্প্রিং-এর ওজনকলে তা হবে না। অর্থাৎ আপনার কাছে যদি দাঁড়িপাল্লার ওজনে দশ পাউন্ড সিসা থাকে তাহলে দাঁড়িপাল্লায় ওজন করলে পৃথিবীর যে কোনো জায়গায়ই তার ওজন দশ পাউন্ড হবে। কিন্তু লন্ডনে যদি ওজন স্প্রিং-এর কলে দশ পাউন্ড হয় তাহলে উত্তর মেরুতে ওজন হবে বেশি, বিষুবরেখায় হবে কম, বিমানে উঁচুতে উঠলে হবে কম আর কয়লা খনির তলায়ও কম হবে– অবশ্য ঐ সমস্ত জায়গায় যদি একই স্প্রিং-এর কলে ওজন করা হয়। আসলে দুটি যন্ত্র–দুটি একেবারেই ভিন্ন পরিমাণ (quantity) মাপে। দাঁড়িপাল্লা যা মাপে তাকে বলা হয় [এখন আমরা যে পরিমার্জনা (refinement) বিচার করব সেটা বাদ দিলে] পদার্থের পরিমাণ। এক পাউন্ড সীসা আর এক পাউন্ড পালকে একই পরিমাণ পদার্থ রয়েছে। প্রমাণ ‘ওজন’ আসলে প্রমাণ ‘ভর। দাঁড়িপাল্লার অন্য দিকটায় যে কোনো বস্তু চাপিয়ে দিয়ে সেই বস্তুর ভর এগুলি দিয়ে মাপা হয়। ওজন কিন্তু এমন একটি ধর্ম যার কারণ পৃথিবীর মহাকর্ষ । এটা হল সেই পরিমাণ বল যা দিয়ে পৃথিবী একটি বস্তুপিণ্ডকে আকর্ষণ করে। স্থান থেকে স্থানান্তরে এই বলের পরিবর্তন হয়। প্রথমত পৃথিবীর বাইরে যে কোনো জায়গায় এই বল পৃথিবীর কেন্দ্র থেকে তার দূরত্বের বর্গের ব্যস্তপরিবর্তী (varies inversely)। সুতরাং বেশি উঁচুতে এ বল কম। দ্বিতীয়ত, আপনি যখন কয়লা খনির তলায় যান পৃথিবীর খানিকটা অংশ থাকে আপনার উপরে এবং পদার্থকে নিচে আকর্ষণ না করে উপরে আকর্ষণ করে ফলে নিচের দিকে মোট আকর্ষণ ভূ-পৃষ্ঠের তুলনায় কম। তৃতীয়ত, পৃথিবীর আবর্তনের দরুন সৃষ্টি হয় ‘অপকেন্দ্র’ বল (centrifugal force)–সে বল মহাকর্ষের বিরুদ্ধে ক্রিয়া করে। অপকেন্দ্র বল সবচাইতে বেশি বিষুবরেখায় কারণ আবর্তনের ফলে সেখানেই বেগ সবচাইতে বেশি। মেরু প্রদেশে এ বলের অস্তিত্ব নেই কারণ মেরুগুলি আবর্তনের অক্ষে অবস্থিত। এই সমস্ত কারণে একটি বস্তুপিণ্ডকে যে বল দিয়ে পৃথিবী আকর্ষণ করে সে বল এক এক জায়গায় এক এক রকম। এবং এ পার্থক্য মাপনযোগ্য। স্প্রিং-এর মাপন যন্ত্র এই বলই মাপে। এই জন্যই স্প্রিং-এর যন্ত্রের মাপনফল এক এক জায়গায় এক এক রকম। দাঁড়িপাল্লায় যে বস্তুপিণ্ড ওজন করা হবে সেটা এবং প্রমাণ বাটখারা একই রকম পরিবর্তিত হয়। সুতরাং দাড়িপাল্লার ক্ষেত্রে মাপনফল সর্বত্রই সমান কিন্তু এই মাপনফল ওজন নয় আসলে এটা ভর। একটি প্রমাণ ওজনের ভর সর্বত্রই এক কিন্তু ওজন সর্বত্র এক নয়। আসলে এটা ভরের একক (unit) ওজনের নয়। একটি বিশেষ বস্তুপিণ্ডের ভর অপরিবর্তী (invariable)। তাত্ত্বিক উদ্দেশ্যে ভরের গুরুত্ব ওজনের চাইতে অনেক বেশি। পরিস্থিতি অনুসারে ওজনের পরিবর্তন হয়। শুরুতে ভরকে ‘পদার্থের পরিমাণ’ বলে ভাবা যেতে পারে। পরে আমরা দেখব এ দৃষ্টিভঙ্গিও সম্পূর্ণ নির্ভুল নয় কিন্তু পরবর্তী পরিমার্জন (refinements) শুরু করার জন্য শুরুতে এই অর্থে আমাদের কাজ চলতে পারে।

তাত্ত্বিক উদ্দেশ্যে ভরের সংজ্ঞা নির্ধারিত হয় একটি নির্দিষ্ট ত্বরণ সৃষ্টি করতে যে পরিমাণ বল প্রয়োজন হয় তাই দিয়ে : একটি বস্তুপিণ্ডের ভর যত বেশি হবে একটি নির্দিষ্ট কালে তার বেগের একটি নির্দিষ্ট পরিমাণ পরিবর্তন আনতে তার তত বেশি বলের প্রয়োজন হবে। একটি হ্রস্ব রেলগাড়ির তুলনায় একটি দীর্ঘ রেলগাড়ির প্রথম আধ মিনিটে ঘণ্টায় দশ মাইল বেগ লাভ করতে অনেক বেশি শক্তিশালী ইঞ্জিন প্রয়োজন হবে। কিংবা আমাদের এমন পরিস্থিতি হতে পারে যেখানে বিভিন্ন বস্তৃপিণ্ড সাপেক্ষ বল অভিন্ন। সেক্ষেত্রে আমরা সেগুলিতে উৎপন্ন ত্বরণ মেপে তাদের ভরের পারস্পরিক অনুপাত বলতে পারি : ভর যত বেশি, ত্বরণ তত কম। এই পদ্ধতির দৃষ্টান্ত হিসাবে আমরা অপেক্ষবাদের পক্ষে গুরুত্বপূর্ণ একটি উদাহরণ দিতে পারি। তেজস্ক্রিয় বস্তুপিণ্ডগুলি থেকে বিরাট বেগে ইলেকট্রন নির্গত হয়। জলীয় বাষ্পের ভিতর দিয়ে চালালে সেগুলি যাত্রাপথে মেঘ সৃষ্টি করে। এইভাবে আমরা তাদের যাত্রাপথ পর্যবেক্ষণ করতে পারি। একই সময় আমরা তাদের উপর জানিত বৈদ্যুতিক আর চৌম্বক বল প্রয়োগ করতে পারি এবং এই বলগুলির দ্বারা তারা ঋজুরেখা ছেড়ে কতটা বক্র হয়– সেটা পর্যবেক্ষণ করতে পারি। এইভাবে তাদের ভরের তুলনা করা সম্ভব হয়। নিশ্চল পর্যবেক্ষকের মাপ অনুসারে তাদের গতি যত দ্রুততর ভরও তাদের তত বৃহত্তর। এছাড়া অন্যভাবে জানা আছে গতির অভিক্রিয়া বাদ দিলে সমস্ত ইলেকট্রনের ভরই এক।

অপেক্ষবাদ আবিষ্কারের আগে এ সমস্তই জানা ছিল কিন্তু অপেক্ষবাদ দেখিয়েছে চিরায়ত কল্পনে ভরের উপর যে নির্দিষ্ট নিশ্চিত অর্থ আরোপ করা হয়েছিল সত্যিই সে নিশ্চিতি তার ছিল না। ভরকে ভাবা হতো ‘পদার্থের পরিমাণ এবং মনে করা হতো ভর একেবারেই অপরিবর্তী (quite invariable)। এখন কিন্তু দেখা গেল দৈর্ঘ্য এবং কালের মতো ভরও পর্যবেক্ষক-নির্ভর (relative to the observer) এবং ঠিক একই অনুপাতে গতির দ্বারা পরিবর্তিত হয়। এরও কিন্তু প্রতিকার আছে, আমরা সঠিক ভর ঠিক করতে পারি। সেটা হবে বস্তুপিণ্ডের সঙ্গে সঙ্গতিসম্পন্ন পর্যবেক্ষকের মাপন অনুসারে। দৈর্ঘ্য এবং কালের ক্ষেত্রে যেরকম, সেই একই অনুপাতে নিয়ে মাপিত বল থেকে সহজেই এ অনুমিতি হয়েছিল (was easily inferred)।

কিন্তু আরো একটি অদ্ভুত ব্যাপার রয়েছে : এই সংশোধনের পরও কিন্তু আমরা এমন কোনো রাশি পাই না যেটা একই বস্তুপিণ্ড সম্পর্কে সর্বকালে অভিন্ন। একটি বস্তুপিণ্ড যখন শক্তি শোষণ করে–উদাহরণ : তপ্ততর হয়ে তখন তার ‘সঠিক ভর’ (proper mass) সামান্য বৃদ্ধি পায়। এ বৃদ্ধি অতি সামান্য। এ মাপা হয় শক্তির বৃদ্ধিকে আলোকের বেগের বর্গ দিয়ে ভাগ করে। অন্যদিকে আবার একটি বস্তুপিণ্ড শক্তি পরিত্যাগ করলে তার ভর হ্রাস পায়। এ বিষয়ে সবচাইতে উল্লেখযোগ্য ব্যাপার হল : চারটি হাইড্রোজেন পরমাণু সংযুক্ত হয়ে একটি হিলিয়াম পরমাণু গঠন করে কিন্তু তাদের ভর হাইড্রোজেন পরমাণুর ওজনের চারগুণের চাইতে কম। এই পরিঘটনার ব্যবহারিক গুরুত্ব সবচাইতে বেশি। মনে হয় তারকার অভ্যন্তরে এই ব্যাপারটা ঘটে। তার ফল–শক্তি–সে শক্তি আমরা দেখতে পাই তারকার আলোকরূপে। সূর্যের ক্ষেত্রে এই শক্তিই পার্থিব জীবনকে ধারণ করে। পার্থিব পরীক্ষাগারেও এ ক্রিয়া সম্ভব। তার ফলে আমোক এবং তাপরূপে বিরাট পরিমাণ শক্তি মুক্ত হয়। এইভাবেই সম্ভব হয় হাইড্রোজেন বোমা তৈরি। কার্যত এই বোমার আকার এবং ধ্বংস করার ক্ষমতা সীমাহীন। সাধারণ পারমাণবিক বোমা ক্রিয়া করে ইউরেনিয়াম বিঘটনের (disintegration) সাহায্যে। এ বোমার একটি স্বাভাবিক সীমা রয়েছে। এক জায়গায় খুব বেশি ইউরেনিয়াম জমা করলে বিস্ফোরিত হওয়ার জন্য অপেক্ষা না করে বোমাটি নিজে নিজেই বিস্ফোরিত হতে পারে। সেইজন্য একটি বিশেষ বৃহত্তম আকারের চাইতে বড় ইউরেনিয়াম বোমা বানানো সম্ভব নয়। কিন্তু একটা হাইড্রোজেন বোমাতে আমাদের যতটা ইচ্ছা ততটা হাইড্রোজেন থাকতে পারে, কারণ হাইড্রোজেন নিজে নিজে বিস্ফোরিত হয় না। শুধুমাত্র যখন সাধারণ ইউরেনিয়াম বোমার সাহায্যে হাইড্রোজেনে বিস্ফোরণ ঘটানো হয় তখনই হাইড্রোজেন সংযুক্ত হয়ে শক্তি মুক্ত করে। তার কারণ শুধুমাত্র অত্যন্ত উচ্চতাপেই সংযুক্তি সম্ভব।

আর একটি সুবিধা আছে : এই গ্রহে (পৃথিবীতে) ইউরেনিয়ামের সরবরাহ সীমিত সুতরাং ভয় হতে পারে মনুষ্যজাতি ধ্বংস হওয়ার আগেই ইউরেনিয়াম শেষ হয়ে যেতে পারে। কিন্তু হাইড্রোজেনের সরবরাহ কার্যত সীমাহীন এবং এই হাইড্রোজেন ব্যবহার করা যায়। সুতরাং মনুষ্যজাতি নিজেকে ধ্বংস করবে এ আশা করার যথেষ্ট কারণ আছে। ফলে যে সমস্ত কম হিংস্র জীবের বাঁচার সম্ভাবনা তাদের বিরাট সুবিধা হবে।

কিন্তু এবার কম খুশীর খবরে ফিরে আসবার সময় হয়েছে।

আমাদের তাহলে দু’রকম ভর রয়েছে। তার একটিও পুরানো আদর্শের সঙ্গে মেলে না। আলোচ্য বস্তুপিণ্ড গতিশীল একজন পর্যবেক্ষকের মাপা ভর একটি আপেক্ষিক রাশি। বস্তুপিণ্ডের ধর্ম হিসাবে তার কোনো ভৌত গুরুত্ব নেই। ‘আসল ভর’ (proper mass) বস্তুপিণ্ডের পর্যবেক্ষক নিরপেক্ষ একটি অকৃত্রিম ধর্ম। এটাও কিন্তু যথাযথ অপরিবর্তী (strictly constant) নয়। শীঘ্রই আমরা দেখব ভর সম্পর্কিত ধারণা শক্তি সম্পর্কিত ধারণার অঙ্গীভূত হয়ে যায়। বলতে গেলে একটি বস্তুপিণ্ড প্রদর্শিত শক্তির বৈপরীত্যে তার নিজের অভ্যন্তরে যে শক্তি ব্যয় করে, ভর তারই প্রতিরূপ।

ভরের নিত্যতা (conservation),ভরবেগের নিত্যতা এবং শক্তির নিত্যতা ছিল চিরায়ত বলবিদ্যার মহান নীতি। এইবার বিচার করা যাক ভরবেগের নিত্যতা।

বিশেষ অভিমুখে একটি বস্তুপিণ্ডের ভরবেগ হল সেই অভিমুখে তার বেগ এবং তার ভরের গুণফল। সুতরাং ধীর গতিতে চলমান একটি ভারী বস্তুপিণ্ড এবং দ্রুত গতিতে চলমান একটি হালকা বস্তুপিণ্ডের ভরবেগ একই হতে পারে। একাধিক বস্তুপিণ্ডের ভিতরে যখন যে কোনোরকম পারস্পরিক প্রতিক্রিয়া হয়, যেমন সংঘর্ষ কিংবা পারস্পরিক মহাকর্ষ, তখন যে কোনো অভিমুখে সবগুলি বস্তুপিণ্ডের মোট ভরবেগ একই থাকে। অবশ্য যতক্ষণ পর্যন্ত বহিরাগত কোনো প্রভাব এর ভিতরে প্রবেশ না করে। অপেক্ষবাদেও এই বিধির সত্যতা স্বীকৃত। বিভিন্ন পর্যবেক্ষক সাপেক্ষ ভর ভিন্ন ভিন্ন হবে কিন্তু পার্থক্য হবে বেগেরও। এই দুটি পার্থক্য পরস্পরকে অক্রিয় (neutralise) করে দেয়। ফলস্বরূপ : নীতিটির সত্যতা থেকে যায়।

একটি বস্তুপিণ্ডের ভরবেগ বিভিন্ন অভিমুখে বিভিন্ন। একটি বস্তুপিণ্ডের একটি নির্দিষ্ট দিকে গতিবেগের (পর্যবেক্ষকের মাপা) সঙ্গে তার ভরকে (পর্যবেক্ষকের মাপা) গুণ দিয়ে সাধারণত তার ভরবেগ মাপা হয়। বিশেষ অভিমুখে, এক একক কালে অতিক্রম করা দূরত্বকে বেগ বলে। ধরুন এর বদলে আমরা গ্রহণ করলাম বস্তুপিণ্ডটি এক একক অন্তর চলাকালে ঐ অভিমুখে অতিক্রান্ত দূরত্ব। [ সাধারণ ক্ষেত্রে এ পরিবর্তন অতি সামান্য। কারণ বেগ আলোর বেগের চাইতে অনেক কম হলে অতিক্রান্ত কাল (lapse of time) এবং অন্তর প্রায় সমান] আর অনুমান করা যাক পর্যবেক্ষকের মাপা ভরের বদলে আমরা সঠিক ভর’ (prpper mass) বিচার করছি। এই দুটি পরিবর্তনের ফলে একই অনুপাতে বেগ বাড়ে এবং ভর কমে। সুতরাং ভরবেগ একই থাকে। কিন্তু পর্যবেক্ষক অনুসারে পরিবর্তী রাশিগুলির স্থলে প্রতিস্থাপিত হয়েছে পর্যবেক্ষক নিরপেক্ষ স্থিরীকৃত রাশি–অবশ্য সেই নির্দিষ্ট অভিমুখে বস্তুপিণ্ড যে দূরত্ব অতিক্রম করেছে সেটা বাদে।

যখন আমরা কালের স্থলে স্থান-কাল উপস্থাপন করি তখন দেখতে পাই মাপিত ভর (আসল ভরের বৈপরীত্যে), নির্দিষ্ট অভিমুখে ভরবেগের মতো একই ধরনের একটি রাশি। একে বলা যেতে পারে কালাভিমুখী ভরবেগ। অচর ভারকে (invariant mass) এক একক অন্তর অতিক্রম করার সময় অতিক্রান্ত কাল দিয়ে গুণ করে মাপিত ভর পাওয়া যায়। একই অচর ভরকে একক অন্তর ভ্রমণে অতিক্রান্ত দূরত্ব (in the given direction–এই নির্দিষ্ট অভিমুখে) দিয়ে গুণ করলে ভরবেগ পাওয়া যায়। স্থান-কালের দৃষ্টিভঙ্গি থেকে এগুলি স্বাভাবিক ভাবেই সমগোত্রীয় (belong together)।

যদিও, একটি বস্তুপিণ্ডের মাপিত ভর নির্ভর করে বস্তুপিণ্ডটি সাপেক্ষ পর্যবেক্ষক কিভাবে চলমান তার উপর, তবুও এই রাশিটি খুবই গুরুত্বপূর্ণ। মাপিত ভরের নিত্যতা এবং শক্তির নিত্যতা অভিন্ন। ব্যাপারটা বিস্ময়কর মনে হতে পারে কারণ প্রথম দৃষ্টিতে শক্তি এবং ভর বস্তু হিসাবে খুবই পৃথক। কিন্তু দেখা গিয়েছে মাপিত ভর এবং শক্তি একই জিনিস। কি করে এটা হয় সে ব্যাখ্যা সহজ নয় কিন্তু আমরা চেষ্টা করব।

সাধারণের ভাষায় ভর’ এবং শক্তি কোনোক্রমেই এক অর্থ বহন করে না। আমাদের কাছে ভর’ শব্দটা জড়িত চেয়ারে বসা একটি মোটা লোক সম্পর্কীয় ধারণার সঙ্গে আর শক্তি’ শব্দ জড়িত ছিপছিপে, চটপটে, উৎসাহী একটি লোক সম্পর্কিত সাধারণ ভাষার দৃষ্টিভঙ্গি একপেশে (one sided)। সাধারণ ভাষায় এর অর্থের ভিতরে চলা শুরু করতে দেরী হওয়া রয়েছে কিন্তু থামতে দেরী হওয়া নেই অথচ জড়ত্বের সঙ্গে থামতে দেরী হওয়াও জড়িত।

উনবিংশ শতাব্দীর শেষার্ধে বিরাট গুরুত্ব দেওয়া হয়েছিল শক্তির নিত্যতা অথবা বলের স্থায়িত্বের’ (persistence of force) উপর। হার্বার্ট স্পেন্সারের পছন্দ ছিল শেষেরটা। শক্তির রূপ নানারকম হওয়ার দরুন এ নীতি সরল ভাবে বলা সহজ নয় তবে এর সারার্থ হল : শক্তি রূপান্তরিত হতে পারে কিন্তু ধ্বংসও হতে পারে না, সৃষ্টও হতে পারে না, শুধুমাত্র রূপান্তরিত হতে পারে। জ্বলের ‘তাপের যান্ত্রিক তুল্যাঙ্ক’ (mechanical equivalent of heat) আবিষ্কারের মাধ্যমে এই নীতি প্রতিষ্ঠা লাভ করে। এই আবিষ্কারে দেখা গিয়েছিল যে–একটি নির্দিষ্ট পরিমাণ তাপ উৎপাদনের জন্য প্রয়োজনীয় কার্য এবং একটি নির্দিষ্ট উচ্চতায় একটি নির্দিষ্ট ওজনকে তুলবার জন্য প্রয়োজনীয় কার্যের ভিতরে একটি অচর (constant) অনুপাত রয়েছে। আসলে যান্ত্রিক ব্যবস্থা অনুসারে দুটির ভিতরে যে কোনো একটির উদ্দেশ্যে একই ধরনের কার্য ব্যবহার করা সম্ভব। যখন দেখা গেল তাপের উপাদান অণুগুলির গতি, তখন তাপ যে অন্য শক্তির সদৃশ এ তথ্য স্বাভাবিক মনে হয়েছিল। মোটামুটি বলতে গেলে একটি বিশেষ পরিমাণ তত্ত্বের সাহায্যে শক্তির সমস্ত রূপকেই পরিণত করা হয়েছিল দুটোতে। সেগুলির নাম ছিল যথাক্রমে স্থৈতিক শক্তি (potential energy) এবং গতীয় শক্তি (kinetic energy)। তাদের সংজ্ঞা ছিল নিম্নরূপ :

একটি বস্তুকণার ভরের অর্ধেকের সঙ্গে বেগের বর্গের গুণফল সেই বস্তুকণার গতীয় শক্তি। কয়েকটি বস্তুকণার গতীয় শক্তি বিচ্ছিন্নভাবে প্রতিটি বস্তুকণার গতীয় শক্তির যোগফলের সমান।

স্থৈতিক শক্তির সংজ্ঞা আরো শক্ত। শুধুমাত্র বল প্রয়োগের সাহায্যে যাকে রক্ষা করা যায় সেই ম ম যে কোনো ততির অবস্থা (state of strain) স্থৈতিক শক্তির প্রতিরূপ। সহজতম উদাহরণ : একটি ওজনকে যদি একটি উচ্চতায় উঠিয়ে ঝুলিয়ে রাখা হয় তাহলে তার স্থৈতিক শক্তি রয়েছে। তার কারণ ছেড়ে দিলে সেটা পড়ে যাবে। যে উচ্চতায় তোলা হয়েছিল সেই দূরত্ব দিয়ে পড়বার সময় ওজনটি যে গতীয় শক্তি লাভ করবে এর স্থৈতিক শক্তি তার সমান। সেই রকম : একটি ধূমকেতু অত্যন্ত উৎকেন্দ্রিক একটি কক্ষে সূর্যকে প্রদক্ষিণ করার সময়, সূর্য থেকে যখন দূরে তখনকার তুলনায় সূর্যের যখন কাছে তখন দ্রুততর চলে। অর্থাৎ ধূমকেতুটি যখন সূর্যের নিকটতর তখন তার গতীয় শক্তি অনেক বেশি। অন্যদিকে : সূর্য থেকে যখন দূরতম তখন ওর স্থৈতিক শক্তি সবচাইতে বেশি। তার কারণ ধূমকেতুটির অবস্থা তখন উঁচুতে তোলা পাথরটির মতো। কোনো সংঘর্ষ না হলে কিংবা ধূমকেতুটি থেকে খানিকটা পদার্থ বিচ্ছিন্ন না হলে তার গতীয় শক্তি এবং তার স্থৈতিক শক্তির যোগফল অচর (constant)। এক অবস্থান থেকে অন্য অবস্থানে যাওয়ার সময়কার স্থৈতিক শক্তির পরিবর্তন আমরা নির্ভুলভাবে নির্ধারণ করতে পারি কিন্তু এ শক্তির মোট পরিমাণ খানিকটা যাদুচ্ছিক। তার কারণ : শূন্য স্তর (zero level) আমরা স্থির করতে পারি নিজেদের ইচ্ছামতো। উদাহরণ : আমাদের পাথরটি ভূপৃষ্ঠে পতনের সময় কিংবা একটি কূপ দিয়ে পৃথিবীর কেন্দ্রে পতনের সময় কিংবা আরোপিত যে কোনো স্বল্পতর দূরত্বে পতনের সময় যে গতীয় শক্তি সংগ্রহ করবে আমরা মনে করতে পারি সেটাই তার স্থৈতিক শক্তি। আমাদের সিদ্ধান্তে যতক্ষণ আমরা অচল ততক্ষণ পর্যন্ত কোনটা আমরা গ্রহণ করছি তাতে কিছু এসে যায় না। আমরা করছি একটা লাভ ক্ষতির হিসাব সুতরাং কি পরিমাণ সম্পদ নিয়ে শুরু করেছি তাতে কিছু এসে যায় না।

নির্দিষ্ট একগুচ্ছ বস্তুপিণ্ডের গতীয় শক্তি এবং স্থিতীয় শক্তি দুটোই ভিন্ন পর্যবেক্ষক সাপেক্ষ ভিন্ন হবে। চিরায়ত গতিবিদ্যা অনুসারে পর্যবেক্ষকের গতির অবস্থা অনুসারে গতীয় শক্তির পার্থক্য হতো কিন্তু পার্থক্যজ্ঞাপক রাশিটি হতে অচর”। স্থিতীয় শক্তির কোনো পার্থক্য হতো না। সুতরাং সংশ্লিষ্ট পর্যবেক্ষকরা নিজেরা ঋজুরেখায় সমবেগে চলমান এই অনুমান করলে কিংবা তা না হলে, এইভাবে চলমান কোনো বস্তুপিণ্ডকে তাদের গতি আরোপ করতে পারেন এই অনুমান করলে, প্রতিটি পর্যবেক্ষক সাপেক্ষই মোট শক্তি ছিল অচর (constant)। কিন্তু অপেক্ষবাদের গতিবিদ্যায় ব্যাপারটা আরো জটিল। গতীয় শক্তি এবং স্থৈতিক শক্তি সম্পর্কীয় নিউটনীয় ধারণাকে বিশেষ কোনো অসুবিধা ছাড়াই বিশিষ্ট অপেক্ষবাদের সঙ্গে মানিয়ে নেওয়া যায়। কিন্তু স্থৈতিক শক্তির ধারণাকে ব্যাপক অপেক্ষবাদের সঙ্গে মানিয়ে নিয়ে বিশেষ সুবিধা হয় না। একক বস্তুপিণ্ডের ক্ষেত্রে ছাড়া অন্য কোনো ক্ষেত্রে স্থৈতিক শক্তি সম্পর্কীয় ধারণার সাধারণীকরণও সম্ভব নয়। সুতরাং সাধারণ নিউটনীয় অর্থে শক্তির নিত্যতা সম্পৰ্কীয় ধারণার যথার্থতা রক্ষা করা সম্ভব নয়। তার কারণ একটি বস্তুপিণ্ডতন্ত্রের গতীয় এবং স্থৈতিক শক্তি, স্থান-কালের বিস্তৃততর অঞ্চলে আরোপিত সহজাত কল্পন। অষ্টম অধ্যায়ের ব্যাখ্যা করা, স্থানাঙ্ক নির্বাচনের অতি বিরাট স্বাধীনতা (latitude) এবং স্থানকালের পাহাড়ি চরিত্র যুক্তভাবে ব্যাপাক অপেক্ষবাদে এই ধরনের কল্পন উপস্থাপনকে অতীব বেমানান করে তোলে। ব্যাপক অপেক্ষবাদে একটি নিত্যতা বিধি রয়েছে কিন্তু এ বিধি নিউটনীয় বলবিদ্যার এবং বিশিষ্ট অপেক্ষবাদের নিত্যতা বিধিগুলির মতো অতটা কার্যকর নয়। তার কারণ, এ বিধি স্থানাঙ্ক নির্বাচনের এমন পদ্ধতির উপর নির্ভরশীল যে পদ্ধতি বোঝা খুবই কঠিন। আমরা দেখেছি স্থানাঙ্ক নির্বাচনের স্বাধীনতা ব্যাপক অপেক্ষবাদের একটি নির্দেশক নীতি। এই নীতির সঙ্গে দ্বন্দ্বের জন্যই নিত্যবিধি সন্দেহভাজন। এর অর্থ : এতদিন যা ভাবা হতো নিত্যবিধির মূলগত গুরুত্ব তার চাইতে কম কিনা অথবা তত্ত্বের গাণিতিক জটিলতার ভিতরে আরো সন্তোষজনক নিত্যবিধি এখনো লুকিয়ে আছে কিনা–এ সমস্যার সমাধান এখনো হয়নি। আপাতত ব্যাপকতত্ত্বে আমাদের শুধুমাত্র একক একটি বস্তুকণার গতীয় শক্তি সম্পর্কীয় কল্পন নিয়েই সন্তুষ্ট থাকতে হবে। পরবর্তী বিচারে শুধু এটাই আমাদের প্রয়োজন। এ কথা মনে রাখা উচিত যে শক্তির নিত্যতা সম্পর্কে এই সমস্ত অসুবিধা ব্যাপকতত্ত্বেই দেখা যায়, বিশিষ্ট তত্ত্বে নয়। যেখানে মহাকর্ষকে অগ্রাহ্য করা যায় এবং বিশিষ্ট তত্ত্ব প্রয়োগ সম্ভব সেখানেই শক্তির নিত্যতা রক্ষা সম্ভব।

কার্যক্ষেত্রে নিত্যতার অর্থ এবং তত্ত্বক্ষেত্রে নিত্যতার অর্থ ঠিক এক নয়। একটি জিনিসের পরিমাণ যখন যে কোনো এক সময় এবং যে কোনো অন্য সময় একই থাকে তত্ত্বে তখন আমরা বলি রাশিটি (quantity) নিত্য। কিন্তু কার্যক্ষেত্রে আমরা সারা পৃথিবী পুঙ্খানুপুঙ্খরূপে পর্যবেক্ষণ করতে পারি না সুতরাং আর একটু সহজ কোনো অর্থ আমাদের মেনে নিতে হবে। আমরা বোঝাতে চাই : একটি নির্দিষ্ট অঞ্চলে পরিমাণজ্ঞাপক রাশিটির যদি পরিবর্তন হয়, তাহলে তার কারণ, কিছুটা পরিমাণের সীমান্ত অতিক্রম করা। যদি কোনো জন্ম কিংবা মৃত্যু না হয় তাহলে জনসংখ্যা নিত্য হবে। সে ক্ষেত্রে একটি দেশের জনসংখ্যার পরিবর্তনের কারণ হতে পারে দেশবাসীর বিদেশ গমন কিংবা বিদেশীর সে দেশে আগমন অর্থাৎ সীমান্ত অতিক্রম করা। আমরা হয়তো চীন কিংবা মধ্য আফ্রিকার নির্ভুল আদম-শুমারী করতে পারি না সুতরাং আমরা হয়তো পৃথিবীর মোট জনসংখ্যা নির্ধারণ করতে পারি না। কিন্তু যেখানেই পরিসংখ্যান সম্ভব সেখানেই যদি দেখা যায় লোকের সীমান্ত অতিক্রমের জন্য যে পরিবর্তন হয় সে পরিবর্তন ছাড়া জনসংখ্যার কোনো পরিবর্তন হয় না তাহলে জনসংখ্যাকে অচর মনে করা যুক্তিসঙ্গত হবে। আসলে অবশ্য জনসংখ্যা নিত্য নয়। আমার পরিচিত একজন শারীরবিদ (Physiologist) একবার একটা থার্মোস (thermos) চারটে ইঁদুর রেখেছিলেন। কয়েক ঘণ্টা বাদে সেগুলিকে বার করতে গিয়ে তিনি দেখলেন রয়েছে এগারোটা ইঁদুর। কিন্তু ভরের এরকম পরিবর্তন হয় না। শেষকালের ঐ এগারোটা ইঁদুরের ভর শুরুর চারটে ইঁদুরের ভরের চাইতে একটুও বেশি ছিল না।

যে সমস্যার জন্য আমরা শক্তি নিয়ে আলোচনা করছিলাম এ তথ্য আমাদের সেই সমস্যাঁতে ফিরিয়ে নিয়ে এল। আমরা বলেছিলাম অপেক্ষবাদে মাপিত ভর এবং শক্তিকে একই বস্তুরূপে বিচার করা হয় এবং দায়িত্ব গ্রহণ করেছিলাম তার কারণ ব্যাখ্যা করার। এবার সেই ব্যাখ্যা শুরু করার সময় হয়েছে। কিন্তু ষষ্ঠ অধ্যায়ের শেষাংশের মতো এখানেও গণিতে সম্পূর্ণ অজ্ঞ পাঠক এই জায়গাটা বাদ দিয়ে পরবর্তী অনুচ্ছেদ থেকে শুরু করলে ভাল করবেন।

আলোকের বেগকে বেগের এককরূপে গ্রহণ করা যাক। অপেক্ষবাদে এটাই সবসময় সুবিধাজনক। m হোক বস্তুকণাটির সঠিক ভর এবং পর্যবেক্ষক সাপেক্ষ বেগ হোক v।

তাহলে এর মাপিত ভর হবে :

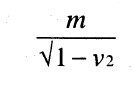
সাধারণ সঙ্কেত অনুসারে এর গতীয় শক্তি কিন্তু হবে :

আমরা আগে দেখেছি শক্তির হিসাব শুধুমাত্র লাভ-ক্ষতির হিসাবের মতো। সুতরাং আমরা এর সঙ্গে খুশীমতো যে কোনো অচর সংখ্যা যোগ করতে পারি। সুতরাং আমরা বলতে পারি শক্তি :

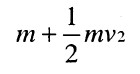
v যদি আলোকের বেগের ক্ষুদ্র ভগ্নাংশ হয় তাহলে m + mv2 প্রায় নির্ভুলভাবে

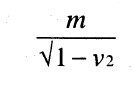
এর সমান। সুতরাং বৃহৎ বস্তুপিণ্ডগুলির যেরকম বেগ থাকে সেই রকম ক্ষেত্রে দেখা যায় মাপনযোগ্য নির্ভুলতার সীমার ভিতরে শক্তি এবং ভরের পার্থক্য করা সম্ভব নয়। আসলে আমাদের শক্তির সংজ্ঞা পরিবর্তন করা ভাল। সেটা হওয়া উচিত–

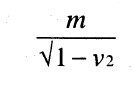
তার কারণ নিত্যতার সদৃশ বিধি সাপেক্ষ এই রশি সত্য; এবং বেগ যখন খুব। বেশি তখন চিরায়ত সঙ্কেতের তুলনায় এই রাশি শক্তির মাপন অনেক ভালভাবে প্রকাশ করে। সুতরাং চিরায়ত সঙ্কেতকে অবশ্যই আসন্ন ভাবা উচিত। নতুন সঙ্কেত তার নির্ভুল রূপ। এইভাবেই শক্তি এবং মাপিত ভর অভিন্ন হয়ে যায়।

এখন আমি কর্ম (action) সম্পৰ্কীয় ধারণা নিয়ে আলোচনা করছি। সাধারণ মানুষের কাছে এ শব্দ শক্তির চাইতে কম পরিচিত। কিন্তু আপেক্ষিক পদার্থবিদ্যা এবং কোয়ান্টাম তত্ত্বে এর গুরুত্ব বেড়েছে। (কোয়ান্টাম হল : অল্প পরিমাণ কর্ম)। শক্তি এবং কালের গুণফল প্রকাশ করার জন্য কর্ম শব্দ ব্যবহার করা হয়। অর্থাৎ একটি তন্ত্রে যদি এক একক শক্তি থাকে তাহলে এক সেকেন্ডে সে এক একক কর্ম প্রয়োগ করবে। একশ’ সেকেন্ডে প্রয়োগ করবে একশ’ একক কর্ম… ইত্যাদি। যে তন্ত্রে একশ’ একক শক্তি আছে সে তন্ত্র এক সেকেন্ডে ১০০ একক কর্ম প্রয়োগ করবে আর ১০০ সেকেন্ডে প্রয়োগ করবে ১০,০০০ একক কর্ম…ইত্যাদি। সুতরাং অযথাযথভাবে প্রকাশ করলে ‘কর্ম’ শব্দের অর্থ কতটা কাজ করা হয়েছে তার একটি মাপ। অধিকতর শক্তি প্রকাশ করলে কিংবা দীর্ঘতর কাল কার্য করলে এটা বৃদ্ধি পায়। যেহেতু শক্তি এবং মাপিত ভর অভিন্ন সুতরাং কর্মকে আমরা মাপিত ভর এবং কালের গুণফল রূপেও প্রকাশ করতে পারি। চিরায়ত বলবিদ্যায় যে কোনো অঞ্চলে পদার্থের ঘনত্ব নির্ণয় করা হয় ভরকে আয়তন দিয়ে ভাগ করে। অর্থাৎ একটি ক্ষুদ্র অঞ্চলের ঘনত্ব যদি আপনার জানা থাকে তাহলে ঘনত্বকে ক্ষুদ্র অঞ্চলের আয়তন দিয়ে গুণ করলে আপনি মোট পদার্থের পরিমাণ জানতে পারবেন। আপেক্ষিক বলবিদ্যায় আমরা সবসময়ই স্থানের জায়গায় স্থান-কাল প্রতিস্থাপন করি। সুতরাং একটি অঞ্চলকে কিছুতেই আর শুধুমাত্র আয়তনরূপে বিচার করা যায় না, বিচার করা হয় কিছুকাল স্থায়ী আয়তনরূপে। একটি ক্ষুদ্র অঞ্চল হবে স্বল্পকাল স্থায়ী একটা ক্ষুদ্র আয়তন। এর ফল : ঘনত্ব জানা থাকলে নতুন অর্থে একটি ক্ষুদ্র অঞ্চলে শুধুমাত্র ক্ষুদ্র ভরই রয়েছে তাই নয়, রয়েছে ক্ষুদ্র ভর এবং স্বল্পকালের গুণফল। অর্থাৎ স্বল্প পরিমাণ ‘কর্ম’। আপেক্ষিক বলবিদ্যায় ‘কর্ম’ কেন মূলগত গুরুত্ব লাভ করবে বলে আশা করা যায় তার ব্যাখ্যা এটাই। আসলে ঘটনাও তাই।

অবাধে চলমান একটি বস্তুকণা একটি ধরাকৃতি অনুগমন করে (follows a geodesic)। এই স্বীকার্যের স্থলে বস্তুকণার কর্ম সম্পর্কীয় তুল্য একটি অনুমান প্রতিস্থাপন করা যায়। এরকম একটি অনুমানে নাম ন্যূনতম ক্রিয়ার সূত্র’ (prin ciple of least action)। এ নীতির বক্তব্য : একটি বস্তুপিণ্ড এক অবস্থা থেকে অন্য অবস্থায় যেতে হলে সেই পথই নির্বাচন করবে যে পথে সামান্য পৃথক অন্য পথের তুলনায় কম কর্ম প্রয়োজন –আবারও মহাজাগতিক আলস্যবিধি (law of cosmic laziness)! ন্যূনতম ক্রিয়ার সূত্রগুলি শুধুমাত্র একক বস্তুপিণ্ডগুলিতেই সীমাবদ্ধ নয়। এমন সমরূপ অনুমান সম্ভব যে অনুমান পর্বত এবং উপত্যকা সমেত সম্পূর্ণ স্থান-কাল বিবরণের পথিকৃৎ অনুমানও। এই নীতিগুলি অপেক্ষবাদ এবং কোয়ান্টাম তত্ত্বে একটি কেন্দ্রীয় ভূমিকা পালন করে। তাছাড়া এই নীতিগুলি বলবিদ্যার শুদ্ধ প্রথানুসারী (formal) অংশগুলি বর্ণনা করার বৃহত্তম ব্যাপ্তিসম্পন্ন উপায় (most comprehensive means)।