০৮. আইনস্টাইনের মহাকর্ষীয় বিধি

৮. আইনস্টাইনের মহাকর্ষীয় বিধি

আইনস্টাইনের বিধি আলোচনার আগে, যৌক্তিক ভিত্তি বিচারে নিউটনের মহাকর্ষীয় বিধি যে সম্পূর্ণ নির্ভুল হতে পারে না সে বিষয়ে আমাদের নিঃসন্দেহ হওয়া ভাল।

নিউটন বলেছেন পদার্থের যে কোনো দুটি কণার ভিতরে একটি বল (force) রয়েছে। এই বল ভর দুটির গুণফলের আনুপাতিক (proportional) এবং তাদের দূরত্বের বর্গের বিষমানুপাতিক (inversely proportional)। অর্থাৎ ভরের প্রশ্ন আপাতত অগ্রাহ্য করলে, বক্তৃকণা দুটি এক মাইল দূরত্বে থাকলে তাদের ভিতরে যে বিশেষ আকর্ষণ থাকবে, দূরত্ব দু মাইল হলে আকর্ষণ হবে তার এক চতুর্থাংশ। যখন তারা তিন মাইল দূরত্বে তখন সেটা হবে ন’ ভাগের একভাগ … এই রকম। দূরত্বের বৃদ্ধির তুলনায় আকর্ষণের হ্রাস অনেক দ্রুত। নিউটন যখন দূরত্বের কথা বলেছেন তখন অবশ্যই তিনি একটি নির্দিষ্ট কালে দূরত্ব বোঝাতে চেয়েছেন। তিনি ভেবেছিলেন কাল বিষয়ে কোনো দ্ব্যর্থ থাকতে পারে না। কিন্তু আমরা দেখেছি এ ধারণা ভুল। একজন পর্যবেক্ষক পৃথিবীতে এবং সূর্যে যে মুহূর্তকে অভিন্ন ভাববেন অন্য একজন সেটাকে ভাববেন দুটি ভিন্ন মুহূর্ত। সুতরাং একটি বিশেষ মুহূর্তের দূরত্ব’ এক ব্যক্তিনিষ্ঠ কল্পন, এ কল্পনের মহাজাগতিক বিধিতে প্রবেশের অধিকার সামান্যই আমরা অবশ্য গ্রিনউইচ পর্যবেক্ষণাগারের মাপন অনুসারে কাল মাপব একথা বলে আমাদের বিধিকে দ্ব্যর্থবোধহীন করতে পারি। কিন্তু পৃথিবীর আকস্মিক পরিস্থিতি এত গুরুত্বের সঙ্গে গ্রহণযোগ্য, এ তথ্য বিশ্বাস করা আমাদের পক্ষে কঠিন। দূরত্বের মাপও বিভিন্ন পর্যবেক্ষক সাপেক্ষ পরিবর্তিত হবে। সুতরাং মহাকর্ষীয় বিধির নিউটনীয় অবয়ব একেবারে নির্ভুল এ কথা মানতে আমরা রাজি নই। তার কারণ একই রকম বিধিসম্মত বহু রীতির ভিতরে যেটি আমরা গ্রহণ করব ফলের পার্থক্য হবে সেই অনুসারে। খুনীর খুনের অপরাধ যদি নির্ভর করে সম্ভাব্য অপরাধীর পরিচয় তার নামে না পদবীতে, তাহলে ব্যাপারটা যেরকম অযৌক্তিক হবে মহাকর্ষীয় বিধির নিউটনীয় বিধির অবয়বও সেইরকমই অযৌক্তিক। দূরত্ব মাইলে মাপা হোক কিংবা কিলোমিটারে মাপা হোক ভৌত বিধিগুলির অভিন্ন হতেই হবে এ তথ্য স্বতঃপ্রতীয়মান এবং মূলগতভাবে একই নীতির যা বিস্তার সেটাই আমাদের বিবেচ্য।

বিশিষ্ট অপেক্ষবাদ যা মেনে নেয় আমাদের মাপন তার চাইতেও বেশি রীতিগত (conventional)। তাছাড়া প্রতিটি মাপনই ভৌত পদার্থের সাহায্যে করা একটি ভৌত পদ্ধতি। তার ফল নিশ্চয়ই হবে একটি পরীক্ষালব্ধ উপাত্ত। কিন্তু যে সরল অর্থ তার উপর আমরা আরোপ করি সে উপাত্তের ব্যাখ্যা অত সরল নাও হতে পারে। সুতরাং কোনো কিছু কি করে মাপতে হয় সেটা আমরা জানি, শুরুতে এ ঘোষণা আমরা করব না। আমরা ধরে নিচ্ছি অন্তর নামক একটি ভৌত রাশি রয়েছে, সে রাশি এমন দুটি ঘটনার সম্পর্ক প্রকাশ করে যে ঘটনা দুটির পারস্পরিক বিচ্ছিন্নতা অত্যন্ত বেশি নয়। কিন্তু সেটা মাপতে জানি এ মাননা আমরা আগে থেকে করছি না। তবে এর আগের অধ্যায়ে যেরকম বলা হয়েছে পিথাগোরাসের উপপাদ্যের সেরকম কোনো একটি সাধারণীকরণ থেকে এটা পাওয়া যায় শুধুমাত্র এইটুকু আমরা মানছি।

তবে আমরা কিন্তু ঘটনাগুলির একটি ক্রম অনুমান করি (assume order) এবং অনুমান করি এ ক্রম চারমাত্রিক। অর্থাৎ আমরা অনুমান করছি : একটি ঘটনা তৃতীয় একটির তুলনায় অন্য একটির নিকটতর এ কথার অর্থ আমরা জানি সুতরাং নির্ভুল মাপনের আগে একটি ঘটনার সান্নিধ্য (neighbourhood) সম্পর্কে আমরা বলতে পারি। তাছাড়া আমরা অনুমান করছি স্থান-কালে একটি ঘটনার অবস্থান আরোপ করতে হলে চারটি রাশি (স্থানাঙ্ক) প্রয়োজন। যথা : আগে উল্লেখ করা বিমানে বিস্ফোরণের ব্যাপারে প্রয়োজন অক্ষাংশ, দ্রাঘিমা, উচ্চতা এবং কাল। কিন্তু এই স্থানাঙ্কগুলি কি করে আরোপ করা হল সে সম্পর্কে কোনো মাননা আমরা করছি না। শুধুমাত্র আমরা মানছি সান্নিধ্যের ঘটনাগুলি সম্পর্কে সান্নিধ্যের স্থানাঙ্কগুলি আরোপ করা হয়।

স্থানাঙ্ক নামক এই সংখ্যাগুলি আরোপের পদ্ধতি সম্পূর্ণ যাদৃচ্ছিকও নয় আবার সযত্ন মাপনের ফলও নয়। এর অবস্থান মাঝামাঝি। আপনি যখন অবিচ্ছিন্ন গতিতে চলেছেন তখন আপনার স্থানাঙ্কগুলি অবশ্যই কখনো হঠাৎ লাফিয়ে পরিবর্তিত হবে না। আমেরিকাতে দেখা যায় (ধরে নেওয়া যাক) চতুর্দশ রাস্তা এবং পঞ্চদশ রাস্তার সব বাড়িগুলির নম্বর ১৪০০ থেকে ১৫০০ এর ভিতরে হওয়ার সম্ভাবনা আবার পঞ্চদশ এবং ষোড়শ রাস্তার ভিতরকার নম্বর হওয়ার সম্ভাবনা ১৫০০, ১৬০০, এমনকি চৌদ্দ শতকের সমস্ত সংখ্যা যদি ব্যবহৃত না হয়ে থাকে তাহলেও। আমাদের কাজ এভাবে হবে না কারণ একটি ব্লক থেকে পরের ব্লকে যাওয়ার সময় হঠাৎ লাফ দিতে হয়।

আবার কালিক স্থানাঙ্ক আমরা এইভাবে আরোপ করতে পরি : পরপর দুটি স্মিথ নামক শিশুর জন্মের মধ্যবর্তী কাল বিচার করুন। ইতিহাসে জ্ঞাত ৩০০০ এবং ৩০০১তম স্মিথের জন্মের মধ্যবর্তী সময়ে সংঘটিত একটি ঘটনার স্থানাঙ্ক অবস্থান করবে ৩০০০ থেকে ৩০০১-এর ভিতরে। বছরের যে অংশ ৩০০০তম স্মিথের জন্মের পর গত হয়েছে সেটাই হবে স্থানাঙ্কের ভগ্নাংশ। (স্মিথ পরিবারে পরস্পর দুটো জন্মের মধ্যবর্তী সময় পুরো এক বছর কখনোই হতে পারে না এ তথ্য স্বতঃপ্রতীয়মান)। স্থানাঙ্ক আরোপের এই পদ্ধতি নির্ভুল নিশ্চিত কিন্তু আমাদের উদ্দেশ্য সাধনের উপযুক্ত নয়। কারণ একটি স্মিথের জন্মের ঠিক আগে এবং ঠিক পরে ঘটনাগুলির মাঝে অকস্মাৎ উল্লম্ফন ঘটবে। সুতরাং অবিচ্ছিন্ন যাত্রায় আপনার স্থানাঙ্ক অবিচ্ছিন্ন হবে না। অনুমান করা হচ্ছে অবিচ্ছিন্ন যাত্রা কাকে বলে সেটা মাপন নিরপেক্ষভাবে আমাদের জানা আছে। যখন স্থান-কালে আপনার অবস্থান অবিচ্ছিন্নভাবে পরিবর্তিত হয়। তখন চারটি স্থানাঙ্কের প্রতিটি অবশ্যই অবিচ্ছিন্নভাবে পরিবর্তিত হয়। স্থানাঙ্কগুলির একটি, দুটি কিংবা তিনটির কোনো পরিবর্তন না হতে পারে কিন্তু যে পরিবর্তন হবে সেটা হতে হবে মসৃণ– কোনো আকস্মিক উল্লম্ফন থাকতে পারবে না। স্থানাঙ্ক আরোপের ব্যাপারে অননুমোদনীয় কি রয়েছে সেটা এইভাবে ব্যাখ্যা করা হল।

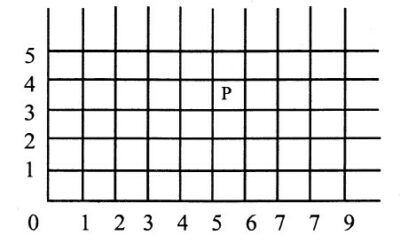
আপনার স্থানাঙ্কগুলির ভিতরে কোন কোন পরিবর্তন বিধিসঙ্গত সে ব্যাখ্যা করার জন্য অনুমান করা যাক আপনি রবারের একটি বড় টুকরো নিয়েছেন। সেটাকে টেনে লম্বা করা হয়নি এরকম অবস্থায় রবারটির উপরে ছোট ছোট বর্গক্ষেত্র আঁকুন। বর্গক্ষেত্রগুলির (square) সবদিকই লম্বায় এক ইঞ্চি দশ ভাগের একভাগ। বর্গগুলির কোণে কোণে একটা করে খুব ছোট পিন লাগান। এই পিনগুলির যে কোনো একটির স্থানাঙ্কগুলির দুটি আমরা নির্ধারণ করতে পারি : একটি নির্দিষ্ট পিন থেকে ডান দিকে গিয়ে উল্লিখিত পিনের ঠিক নিচু অবধি যেতে আমরা যে কটি পিন অতিক্রম করি তার সংখ্যা এবং উপর দিকে ঐ পিন পর্যন্ত যেতে যে কটি পিন অতিক্রম করি তার সংখ্যা। চিত্রে 0 হোক আমাদের প্রারম্ভিক পিন এবং যে পিনের স্থানাঙ্ক আমরা আরোপ করতে চাই সেটা হোক P। P তাহলে P পঞ্চম সার (column) এবং তৃতীয় পর্ভূক্তি (row)। সুতরাং, রবারের তলে (plane) 0-এর স্থানাঙ্ক হবে ৫ এবং ৩।

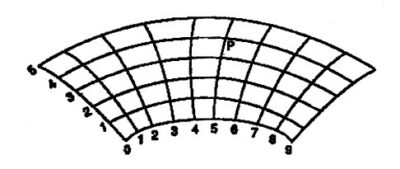
এবার রবারটা আপনি টেনে যত খুশী লম্বা করুন আর পাক দিন। পিনগুলি এবার দ্বিতীয় চিত্রে যেরকম আছে সেইরকম আকার নিক।

আমাদের সাধারণ দৃষ্টিভঙ্গিতে বুঝি ভাগগুলি এখন আর সেই অর্থে দূরত্ব প্রকাশ করে না। কিন্তু স্থানাঙ্কের কাজ ঐ ভাগগুলি দিয়ে একই রকম চলবে। আমরা এখনো বলতে পারি রবারের তলে P-এর স্থানাঙ্ক ৫ এবং ৩। রবারটাকে আমরা এমনভাবে মুড়িয়েছি যে সাধারণত যাকে তল (plane) বলা হয় রবারটা আর সেরকম নেই, তবুও কিন্তু এখনো আমরা রবারটিকে একটি তল বলে ভাবতে পারি। এইরকম অবিচ্ছিন্ন বিকৃতিতে কিছু এসে যায় না।

আর একটি উদাহরণ : আমাদের স্থানাঙ্ক নির্ধারণের জন্য লৌহদণ্ডের পরিবর্তে একটি জ্যান্ত ঈল মাছ* ব্যবহার করা যাক। মাছটা সবসময়ই তার দেহ মোচড়ায়। সেই মুহূর্তে মাছটা যে আকারই ধারণ করুক না কেন, স্থানাঙ্কের দৃষ্টিভঙ্গিতে লেজ থেকে মাথা পর্যন্ত দূরত্বকে এক একক হিসাবে গণনা করা হবে। ঈলটা অবিচ্ছিন্ন তার গা মোড়ানোও অবিচ্ছিন্ন, সুতরাং, স্থানাঙ্ক আরোপের পদ্ধতির জন্য একে আমাদের দূরত্বের একক হিসাবে গ্রহণ করা যেতে পারে। স্থানাঙ্ক আরোপের পদ্ধতির জন্য প্রয়োজন অবিচ্ছিন্নতা। এ পদ্ধতির অন্যান্য অংশ শুধুমাত্র রীতিগত ব্যাপার। সুতরাং জীবন্ত ঈল আর ইস্পাতদণ্ড একই রকম কাজ করবে।

আমরা স্বভাবতই ভাবতে পারি সত্যিকারের সতর্ক মাপনের জন্য জীবন্ত ঈলের চাইতে ইস্পাতদণ্ড ব্যবহার করা ভাল। এটা ঠিক নয়–তার কারণ এ নয় যে ইস্পাতদণ্ড যা বলে ভাবা হতো ঈলও সে কথা বলে কারণ হল ঈলের যে বক্তব্য স্বতঃপ্রতীয়মান ইস্পাতদণ্ড তার চাইতে বেশি কিছু বলে না। ব্যাপারটা আসলে এ নয় যে ঈল সত্যিই অনমনীয় আসলে ইস্পাতদণ্ডও গা মোচড়ায় । আমাদের দৃষ্টিতে যেমন মনে হয় ঈলটা গা মোড়ায় তেমনি গতির সম্ভাব্য একটি অবস্থায় স্থিত একজন পর্যবেক্ষকের মনে হবে ঈল অনমনীয় এবং ইস্পাতদণ্ড গা মোচড়ায় (wriggle)। আমাদের এবং ঐ পর্যবেক্ষকের চাইতে পৃথকভাবে চলমান প্রত্যেকেরই মনে হবে ঈল এবং দণ্ড দুটোই গা মোড়ায় এবং একজন পর্যবেক্ষক সঠিক এবং অন্য পর্যবেক্ষক ভুল একথা বলার কোনো উপায় নেই। এই সমস্ত ক্ষেত্রে যা দেখা যায় সেটা পর্যবেক্ষিত ভৌত পদ্ধতির উপর সম্পূর্ণ নির্ভরশীল নয়। সেটা পর্যবেক্ষকের দৃষ্টিভঙ্গির উপরও নির্ভরশীল। দূরত্ব এবং কাল মাপন মাপিত বস্তুর ধর্ম প্রত্যক্ষভাবে প্রকাশ করে না, প্রকাশ করে বস্তুর সঙ্গে মাপকের সম্পর্ক। সুতরাং ভৌত জগৎ সম্পর্কে পর্যবেক্ষণ যা বলতে পারে সেটা এতদিন পর্যন্ত আমরা যা বিশ্বাস করেছি তার চাইতে অনেক বেশি বিমূর্ত।

প্রাচীন গ্রীক আমল থেকে স্কুলে যে জ্যামিতি পড়ানো হয় তার পৃথক বিজ্ঞান হিসাবে অস্তিত্ব আর রইল না, সেটা মিশে গেল পদার্থবিদ্যার সঙ্গে। এ তথ্য বোঝার গুরুত্ব রয়েছে। প্রাথমিক জ্যামিতির দুটি মূলগত ধারণা ছিল ঋজুরেখা এবং বৃত্ত। আপনার কাছে যেটাকে মনে হয় একটা ঋজুদণ্ড, যার অংশগলির অস্তিত্ব বর্তমানে রয়েছে, আর একজনের কাছে সেটা মনে হতে পারে একটা রকেটের উড়ান অর্থাৎ এমন ধরনের একটি বক্ররেখা যার অংশগুলি ক্রমান্বয়ে অস্তিত্বে উপনীত হচ্ছে।

বৃত্ত নির্ভরশীল দূরত্ব মাপনের উপর–কারণ বৃত্ত আসলে কেন্দ্র থেকে বিশেষ একটি সমদূরত্বে অবস্থিত সমস্ত বিন্দুর সমষ্টি। আমরা দেখেছি দূরত্ব মাপন একটি ব্যক্তিনিষ্ঠ ব্যাপার। সেটা নির্ভর করে পর্যবেক্ষক কিভাবে চলমান তার উপর। মিচেলসন-মর্লির বৈজ্ঞানিক পরীক্ষা বৃত্তের বস্তুনিষ্ঠ সত্যতার অভাব প্রদর্শন করেছে। এক অর্থে এই পরীক্ষা সম্পূর্ণ অপেক্ষবাদের আরম্ভবিন্দু। আমাদের মাপনের জন্য প্রয়োজনীয় অনমনীয় বস্তুপিণ্ড শুধুমাত্র কয়েকজন পর্যবেক্ষক সাপেক্ষই অনমনীয়, অন্য পর্যবেক্ষক সাপেক্ষ তাদের মাত্রা (dimensinate) অবিচ্ছিন্নভাবে পরিবর্তিত হতে থাকবে। শুধুমাত্র আমাদের পৃথিবীবদ্ধ বেয়াড়া (obstinate) কল্পনার জন্যই আমাদের পক্ষে জ্যামিতিকে পদার্থবিদ্যা থেকে বিচ্ছিন্ন মনে করা সম্ভব হয়েছে।

সেইজন্যই শুরু থেকে আমরা আমাদের স্থানাঙ্কগুলিকে (co-ordinates) কোনো ভৌত গুরুত্ব দান করার ঝামেলায় থাকি না। আগে পদার্থবিদ্যায় ব্যবহৃত স্থানাঙ্কগুলিকে সযত্নে মাপা দূরত্ব বলে ভাবা হতো। এখন আমরা বুঝতে পারছি এই প্রাথমিক প্রযত্ন পরিত্যক্ত হয়েছে। যত্নের প্রয়োজন পরের একটি ধাপে। আমাদের স্থানাঙ্কগুলি এখন একাধিক ঘটনার পঞ্জী গঠনে একটি নিয়মানুগত পদ্ধতি ছাড়া বিশেষ কিছু নয়। গণিত শাস্ত্রের টেন্সর পদ্ধতি (tensor-প্রদিশ) বিরাট শক্তিশালী এক সাধনী। এর সাহায্যে আপাতদৃষ্ট অযত্নে আরোপিত স্থানাঙ্কের জন্য সূক্ষ্ম এবং নির্ভুল মাপনের সমস্ত সাধনীই ব্যবহার করা হয়েছে। শুরুতে এলোমলোভাবে কাজ করার সুবিধা এই যে আমরা অজানা (surreptitious) ভৌত অনুমান এড়িয়ে যেতে পারি। প্রথম দিকে যদি ধারণা থাকে যে আমাদের স্থানাঙ্কগুলির কোনো ভৌত গুরুত্ব রয়েছে তাহলে এই অজানা অনুমান এড়ানোর সম্ভাবনা অল্প।

পর্যবেক্ষণ করা সমস্ত ভৌত পরিঘটনা সম্পর্কে অজ্ঞতা নিয়ে অগ্রসর হওয়ার চেষ্টা করার কোনো প্রয়োজন আমাদের নেই। কিছু কিছু জিনিস আমরা জানি। আমরা জানি একটি বিশেষ পদ্ধতিতে স্থানাঙ্কগুলি নির্বাচন করা হলে প্রাচীন নিউটনীয় পদার্থবিদ্যা প্রায় নির্ভুল। আমরা জানি উপযুক্ত স্থানাঙ্ক সাপেক্ষ বিশিষ্ট অপেক্ষবাদ নির্ভুলতার আরো নিকটতর। এই সমস্ত তথ্য থেকে আমরা আমাদের নতুন স্থানাঙ্কগুলি সম্পর্কে কয়েকটি জিনিস আহরণ করতে পারি। এগুলিই যৌক্তিক (অবরোহী) আহরণের সাহায্যে নতুন তত্ত্বের স্বীকার্যরূপে প্রতিভাত হয়।

এই জাতীয় স্বীকার্যরূপে আমরা গ্রহণ করি।

(১) সমীপবর্তী ঘটনাবলীর অন্তর্বর্তী অন্তর (interval), দূরত্ব সম্পর্কে রিম্যান যেরকম ব্যবহার করেছিলেন সেই রকম সাধারণ অবয়ব গ্রহণ করে।

(২) যথোপযুক্ত (sufficiently), ক্ষুদ্র, হাল্কা এবং প্রতিসম (synmetrical) বস্তুপিণ্ডের স্থান-কালে যাত্রাপথ ধরাকৃতি (geodesic), ব্যতিক্রম হতে পারে শুধুমাত্র বস্তুপিণ্ডটির উপর অমহাকর্ষীয় বলের ক্রিয়ার দরুন।

(৩) আলোকরশ্মির যাত্রাপথ ধরাকৃতি– সেটা এমন যে তার যে কোনো দুটি অংশের অন্তর (interval) শূন্য (zero)।

এই স্বীকার্যগুলির প্রত্যেকটির কিছু ব্যাখ্যা প্রয়োজন।

আমাদের প্রথম স্বীকার্যের প্রয়োজন : দুটি ঘটনা যদি ঘনিষ্ঠরূপে সমীপবর্তী হয় (কিন্তু অন্য রকমটা আবশ্যিক নয়– not necessarily otherwise) তাহলে তাদের ভিতরে একটি অন্তর থাকে। তাদের স্থানাঙ্কের পার্থক্যের সাহায্যে এ অন্তর গণনা করা সম্ভব। গণনার জন্য আগের অধ্যায়ে আলোচিত সঙ্কেতের মতো কোনো একটি সঙ্কেত ব্যবহার করা যেতে পারে। অর্থাৎ আমরা স্থানাঙ্কগুলির পার্থক্যের বর্গ এবং গুণফল নিয়ে তাকে যথোপযুক্ত রাশি দিয়ে (suitable amounts) গুণ করি (সাধারণত এগুলি স্থান থেকে স্থানান্তরে পরিবর্তিত হবে) এবং ফলগুলিকে যোগ করি। প্রাপ্ত যোগফল অন্তরের বর্গ। কি রাশি দিয়ে বর্গগুলি এবং গুণফলগুলিকে গুণ দিতে হবে সেটা আমরা আগে থাকতে অনুমান করি না। সেটা আবিষ্কার করা হবে ভৌত পরিঘটনা পর্যবেক্ষণ করে। কিন্তু আমরা জানি স্থান-কালের যে কোনো ক্ষুদ্র অঞ্চলে আমরা এমনভাবে স্থানাঙ্ক নির্বাচন করতে পারি যে আমরা বিশিষ্ট অপেক্ষবাদে যেরকম পেয়েছি অন্তর প্রায় নির্ভুলভাবে সেই বিশেষ অবয়ব গ্রহণ করে। তার কারণ ব্যাপারটা যে এইরকমই হবে গণিত শাস্ত্রের সাহায্যে সেটা বোঝা যায়। সীমিত অঞ্চলে বিশিষ্ট অপেক্ষবাদ প্রয়োগের জন্য অঞ্চলটি মহাকর্ষবিহীন হওয়ার কোনো প্রয়োজন নেই। সমগ্র অঞ্চলে মহাকর্ষের তীব্রতা যদি কার্যত এক হয় তাহলেই চলবে। এর সাহায্যে আমরা যে কোনো ক্ষুদ্র অঞ্চলে বিশিষ্ট অপেক্ষবাদ প্রয়োগের ক্ষমতা লাভ করি। এটা কত ক্ষুদ্র হবে সেটা নির্ভর করে সন্নিহিত অঞ্চলের উপর । ভূ-পৃষ্ঠে এটা এমন ছোট হতে হবে যাতে পৃথিবীর বক্রতা অগ্রাহ্য করা যায়। গ্রহান্তবর্তী স্থানে এটা এমন ছোট হতে হবে যাতে সমগ্র অঞ্চলে সূর্য এবং গ্রহগুলির আকর্ষণ অবধারণীয়ভাবে অপরিবর্তিত থাকে (sensibly constant)। তারকাগুলির অন্তর্বর্তী স্থানে এটা হতে পারে বিরাট। ধরুন দুটি তারকার দূরত্বের অর্ধেক এবং এতেও মাপনযোগ্য ভুল হবে না।

অর্থাৎ মহাকর্ষপ্রদায়ী পদার্থ (gravitating matter) থেকে বহুদূরে আমরা এমনভাবে স্থানাঙ্ক নির্বাচন করতে পারি যাতে প্রায় ইউক্লিডীয় স্থান পাওয়া যায়। আসলে ‘সেখানে বিশিষ্ট অপেক্ষবাদ প্রযোজ্য’ এই কথাই এখানে অন্যভাবে বলা হল। যদিও পদার্থের সান্নিধ্যে অতি ক্ষুদ্র অঞ্চলে আমরা স্থানকে প্রায় ইউক্লিডীয় করতে পারি তবুও যে অঞ্চলে মহাকর্ষ অবধারণীয়রূপে পরিবর্তিত হয় সে অঞ্চলের সম্পূর্ণ এলাকায় সেটা পারি না। যদি পারি তাহলে দ্বিতীয় স্বীকার্যে যে দৃষ্টিভঙ্গি প্রকাশ করা হয়েছে অন্ততপক্ষে সে দৃষ্টিভঙ্গি আমাদের পরিত্যাগ করতে হবে। স্বীকার্যটি হল; মহাকর্ষীয় বলাধীন চলমান বস্তুপিণ্ডগুলি শুধুমাত্র ধরাকৃতি পথে চলে।

আমরা দেখেছি ধরাকৃতিই পৃষ্ঠতলে এক বিন্দু থেকে অন্য বিন্দুতে অঙ্কিত হ্রস্বতম রেখা। উদাহরণ : পৃথিবী পৃষ্ঠে ধরাকৃতিগুলি বৃহৎ বৃত্ত। স্থান-কাল ক্ষেত্রে গণিত একই কিন্তু বাচনিক ব্যাখ্যা একটু অন্যরকম হতে হবে। ব্যাপক অপেক্ষবাদে শুধুমাত্র সন্নিহিত ঘটনাগুলিরই নির্দিষ্ট নিশ্চিত অন্তর রয়েছে। এ অন্তর একটি থেকে অন্যটিতে যাওয়ার গতিপথ নিরপেক্ষ। দূরস্থিত ঘটনাগুলির অন্তর নির্ভর করে যাত্রাপথের উপর। যাত্রাপথকে ক্ষুদ্র ক্ষুদ্র অংশে বিভক্ত করে তার অন্তরগুলি যোগ করে দূরস্থিত ঘটনাগুলির অন্তর গণনা করা হয়। অন্তর যদি স্থানানুরূপ হয় তাহলে একটি বস্তুপিণ্ড এক ঘটনা থেকে অন্য ঘটনায় যেতে পারে না। সুতরাং বস্তুপিণ্ডগুলি কিভাবে চলে সেই বিচার করার সময় আমরা আবদ্ধ থাকি কালানুরূপ অন্তরে। সন্নিহিত ঘটনাগুলি যখন কালানুরূপ তখন মনে হবে পর্যবেক্ষকদের একটি ঘটনা থেকে অন্য ঘটনায় যাওয়ার অন্তর্বর্তী কালই তাদের অন্তর। সুতরাং যারা একটি ঘটনা থেকে অন্য ঘটনায় ভ্রাম্যমাণ তাঁদের বিচারে তাঁদের নিজেদের ঘড়িতে নির্দিষ্ট ভ্রমণকালই হবে দুটি ঘটনার সম্পূর্ণ অন্তর। কোনো কোনো পথে এই কাল হবে দীর্ঘতর আবার কোনো কোনো পথে হবে হ্রস্বতর। তাদের চলার গতি যত মন্থর হবে, ভ্রমণকালও তাঁদের কাছে ততই দীর্ঘ মনে হবে। এটাকে মামুলী বক্তব্য ভাবা কোনোক্রমেই উচিত নয়। আমি একথা বলছি না যে আপনি যদি লন্ডন থেকে এডিনবরা যান তাহলে আপনার গতি মন্থরতর হলে আপনার সময় বেশি লাগবে। আমি যা বলছি সেটা তার চাইতেও অনেক বেশি অদ্ভূত। আমি বলছি : আপনি যদি সকাল দশটায় লন্ডন ছাড়েন এবং সন্ধ্যা সাড়ে ছটা-গ্রিনউইচ সময়ে এডিনবরা পৌঁছান তাহলে আপনার গতি যত মন্থর হবে সময়ও তত বেশি লাগবে– অবশ্য আপনি যদি নিজের ঘড়িতে কাল মাপেন। এ বক্তব্য সত্যিই বেশ পৃথক। পৃথিবীতে স্থিত কোনো ব্যক্তির দৃষ্টিতে আপনার ভ্রমণকাল সাড়ে আট ঘণ্টা। কিন্তু আপনি যদি সৌরজগতে ভ্রাম্যমাণ একটি আলোকরশ্মি হতেন, যদি সকাল দশটায় লন্ডন থেকে যাত্রা শুরু করতেন, যদি বৃহস্পতি, শনি ইত্যাদি থেকে প্রতিফলিত হতে হতে শেষ পর্যন্ত প্রতিফলিত হয়ে এডিনবরায় পৌঁছাতেন সন্ধ্যা সাড়ে ছটায় তাহলে আপনার বিচারে এই ভ্রমণে একেবারে কোনো সময়ই লাগত না। আর আপনি যদি কোনো ঘোরাপথে যেতেন এবং দ্রুততর ভ্রমণের ফলে যদি আপনি ঠিক সময়ে পৌঁছাতেন তাহলে আপনার গতিপথ যত দীর্ঘ হতো, আপনার বিচারে সময়ও তত কম লাগত। আপনার গতি আলোকের গতির যত নিকটতর হতো কাল-সংক্ষেপও অবিচ্ছিন্নভাবে সেই অনুপাতে হতো। এখন আমি বলছি : একটি বস্তুপিণ্ড যখন ভ্রমণ করে তখন তাকে নিজের উপর ছেড়ে দিলে সে সেই গতিপথই নির্বাচন করবে যে পথে দুটি পর্যায় (stage) অতিক্রম করতে সম্ভাব্য দীর্ঘতম কাল লাগবে। সে যদি একটি ঘটনা থেকে অন্য ঘটনায় অন্য কোনো পথে ভ্রমণ করত তাহলে তার নিজস্ব ঘড়ির মাপ অনুসারে সময় লাগত কম। এ কথার অর্থ : বস্তুপিণ্ডগুলিতে তাদের নিজের উপর ছেড়ে দিলে তাদের চলার গতি হবে যত মন্থর সম্ভব। এটা এক ধরনের মহাজাগতিক আলস্যবিধি (law of cosmic laziness)। এ তথ্যের গাণিতিক প্রকাশ হল : তাদের ভ্রমণপথ ধরাকৃতি। এ ক্ষেত্রে ভ্রমণের দুটি ঘটনার মোট অন্তর যে কোনো বিকল্প ভ্রমণ পথের চাইতে বেশি। (এটা বৃহত্তর-ক্ষুদ্রতর নয়– এই ব্যাপারটার কারণ হল : যে ধরনের অন্তর আমরা বিচার করছি তার সাদৃশ্য দূরত্বের চাইতে কালের সঙ্গেই বেশি)। উদাহরণ : লোকে যদি পৃথিবীর বাইরে গিয়ে কিছুকাল ভ্রমণ করে আবার ফিরে আসতে পারত তাহলে তাদের গমনকাল এবং প্রত্যাবর্তন কালের মধ্যবর্তীকাল পৃথিবীবাসীদের তুলনায় যাত্রীদের ঘড়িতে কম হতো। সূর্য প্রদক্ষিণ করার সময় পৃথিবী তার যাত্রাপথে সেই পথই নির্বাচন করে যে পথের যে কোনো অংশ পরিভ্রমণ করতে তার নিজস্ব ঘড়ির অন্যপথে চলমান ঘড়ির তুলনায় বেশি সময় লাগবে। বস্তুপিণ্ডগুলিকে তাদের নিজেদের উপর ছেড়ে দিলে তারা স্থানকালে ধরাকৃতিতে চলমান হয়–এ কথার অর্থ এটাই।

স্থান-কালকে ইউক্লিডীয় বলে মাননা করা হয় না : এ তথ্য স্মরণে রাখা গুরুত্বপূর্ণ। ধরাকৃতিগুলি সাপেক্ষ এর ক্রিয়া হল : স্থান-কাল একটি গ্রাম্য পাহাড়ি এলাকার মতো। একখণ্ড পদার্থের সান্নিধ্যে যেন একটি স্থান-কালের পাহাড় রয়েছে। শীর্ষে না পৌঁছানো পর্যন্ত পাহাড়টা ক্রমশ দূরারোহ হতে থাকে। অনেকটা বোতলের গলার মতো। এটা শেষ হয় একটি খাড়া গিরিচূড়ায়। এর আগে মহাজাগতিক আলস্যবিধির উল্লেখ করা হয়েছে। এই বিধি অনুসারে পাহাড়ের সন্নিধ্যে কোনো বস্তুপিণ্ড এলে সেটা ঋজুভাবে শিখরে যেতে চেষ্টা করবে না– চেষ্টা করবে ঘুরে যেতে। মহাকর্ষ সম্পর্কে আইনস্টাইনের দৃষ্টিভঙ্গির সারমর্ম এটাই। একটি বস্তুপিণ্ড যা করে তার কারণ তার নিজ সান্নিধ্যের স্থান-কালের চরিত্র। দূরস্থিত একটি বস্তুপিণ্ড থেকে উৎসারিত রহস্যজনক কোনো বল তার কারণ নয়।

একটি উপমার সাহায্যে ব্যাপারটাকে সহজ করা যাবে। ধরুন একটা বিরাট সমতলে (plane) এক অন্ধকার রাতে হাতে লুণ্ঠন নিয়ে কয়েকজন লোক নানাদিকে ঘোরাফেরা করছিল। আরো অনুমান করুন সমতলের এক অংশে একটি পাহাড় ছিল আর পাহাড়ের মাথায় ছিল একটি জ্বলজ্বলে আলোকসঙ্কেত। যেমন বিবরণ দেওয়া হয়েছে আমাদের পাহাড়টা হতে হবে সেইরকম অর্থাৎ যত উপরে যাওয়া যায় তত দূরারোহ এবং শেষে একটা খাড়া গিরিশিখর। আমি অনুমান করব সমতলে বিন্দু বিন্দু কয়েকটা গ্রাম ছড়ানো রয়েছে এবং হাতে লণ্ঠন নিয়ে লোকেরা গ্রামের দিকে এবং গ্রাম থেকে এদিক-ওদিক ঘোরাফেরা করছে। এক গ্রাম থেকে অন্য গ্রামে যাওয়ার সহজতম রাস্তায় পথ তৈরি হয়েছে। পাহাড়ের উপর খুব বেশি দূর ওঠা এড়াবার জন্য সবকটা পথই কিন্তু কম-বেশি বাঁকা (curved)। গিরিশিখরের কাছাকাছি জায়গায় গিরিশিখর থেকে খানিকটা দূরের তুলনায় পথগুলির বক্রতা অনেক বেশি। এখন ধরুন একটা বেলুনে চড়ে খুব উঁচু থেকে যতটা সম্ভব ভাল করে এই জিনিসগুলি আপনি দেখছেন–জমিটা আপনি দেখতে পাচ্ছেন না–দেখছেন শুধু লণ্ঠনগুলি আর আলোকসঙ্কেত। একটা পাহাড় রয়েছে কিংবা আলোকসঙ্কেতটা রয়েছে পাহাড়ের উপর, এ সমস্ত তথ্য আপনি জানতে পারবেন না। আপনি দেখতে পাবেন লোকে আলোক সঙ্কেতের কাছে এলে ঋজুপথ থেকে বাইরের দিকে সরে যায়। আপনার ভাবা স্বাভাবিক যে, এর কারণ ঐ আলোকসঙ্কেত। আপনি ভাবতে পারেন ওটা খুব গরম লোকে পুড়ে যাওয়ার ভয় পাচ্ছে। কিন্তু আপনি যদি দিনের আলোক পর্যন্ত অপেক্ষা করেন তাহলে আপনি পাহাড়টা দেখতে পাবেন, বুঝতে পারবেন আলোকসঙ্কেতটা শুধু পর্বতশিখরটা নির্দেশ করছে– হাতে লণ্ঠন নিয়ে যারা ঘুরছে তাদের উপর কোনো প্রভাবই ওর নেই।

এই উপমার আলোকসঙ্কেতটা সূর্যের প্রতিরূপ, হাতে লণ্ঠন লোকেরা প্রতিরূপ গ্রহ এবং ধূমকেতুর। পথ প্রতিরূপ কক্ষপথের (orbit) আর দিবালোকের আবির্ভাব প্রতিরূপ আইনস্টাইনের আবির্ভাবের। আইনস্টাইন বলেছেন, সূর্য স্থানে অবস্থিত নয়–সূর্যের অবস্থান স্থান-কালে। (পাঠককে আমার পরামর্শ : এ তত্ত্বের মানসচিত্র সৃষ্টি করতে যাবেন না কারণ সেটা অসম্ভব)। প্রতিটি বস্তুপিণ্ড প্রতি মুহূর্তে সহজতম পথ অনুসরণ করতে চেষ্টা করে-কিন্তু পর্বতের অস্তিত্বের জন্য সহজতম পথটি ঋজুরেখা নয়। মোরগ যেমন নিজের বিষ্ঠার ঢিবির উপর বসে থাকে তেমনি প্রতিটি বস্তুখণ্ডই তার নিজস্ব ক্ষুদ্র পাহাড়ের শিখর। পাহাড়টাই আমাদের জানা; শিখরের বস্তুখ অনুমান করা হয় সুবিধার জন্য। এ অনুমানের হয়তো কোনো প্রয়োজন নেই, শুধু পাহাড়েই আমাদের কাজ চলতে পারে। লড়ুয়া মোরগটা যেমন, আয়নায় দেখা যে মোরগটাকে দেখে মেজাজ বিগড়ে যায় সেটার সঙ্গে লড়তে পারে না, তেমনি আমরাও আর কারো পাহাড়ে চড়তে পারি না।

আইনস্টাইনের মহাকর্ষীয় বিধির শুধুমাত্র গুণীয় (qualitative) বিবরণ আমি দিয়েছি। আমি নিজেকে যে পরিমাণ গণিত ব্যবহারের অনুমতি দিয়েছি তার চাইতে বেশি পরিমাণ গণিত ব্যবহার না করে মাত্রিক (quantitative) বিবরণ দেওয়া অসম্ভব। সব চাইতে আকর্ষণীয় ব্যাপার হলো এ বিধি আর দূরস্থিত ক্রিয়ার উপর নির্ভরশীল নয়। গ্রহগুলির উপর সূর্য কোনো বলই প্রয়োগ করে না। ঠিক যেমন জ্যামিতি পদার্থবিদ্যায় পরিণত হয়েছে তেমনি এক অর্থে পদার্থবিদ্যা পরিণত হয়েছে জ্যামিতিতে। মহাকর্ষীয় বিধি পরিণত হয়েছে এই জ্যামিতিক বিধিতে : প্রতিটি বস্তুপিণ্ড স্থান থেকে স্থানান্তরে গমনের জন্য সহজতম পন্থা অনুসরণ করে কিন্তু পথে যে সমস্ত পর্বত এবং উপত্যকার সঙ্গে সাক্ষাৎকার হয় সেগুলি বস্তুপিণ্ডটির গতিপথকে প্রভাবিত করে।

আমরা অনুমান করে চলেছি যে বিচার্য বস্তুপিণ্ডটির উপর শুধুমাত্র মহাকর্ষীয় বলগুলিই ক্রিয়া করে। এখন আমাদের বিচার্য মহাকর্ষীয় বিধি। বিদ্যুৎচুম্বকীয় বল কিংবা ঊনপারমাণবিক (sub-atomic) কণামধ্যস্থ বল আমাদের বিচার্য নয়। এই সমস্ত বলগুলিকেই ব্যাপক অপেক্ষবাদের কাঠামোর ভিতরে নিয়ে আসবার অনেক চেষ্টা হয়েছে। এ প্রচেষ্টা আইনস্টাইন নিজে করেছেন। তাছাড়া করেছেন ওয়েইল (Weyl), কালুজা (Kaluza), ক্লাইন (klein) ইত্যাদি আরো অনেকে। কিন্তু এই প্রচেষ্টাগুলির কোনোটাই সম্পূর্ণ সন্তোষজনক হয়নি। আপাতত আমরা এ গবেষণা অগ্রাহ্য করতে পারি। কারণ সমগ্রভাবে কোনো গ্রহের উপরই বিদ্যুৎচুম্বকীয় কিংবা ঊনপারমাণবিক বলগুলির উপলব্ধিযোগ্য কোনো ক্রিয়া নেই। তাদের গতির কারণ বোঝার জন্য শুধুমাত্র মহাকর্ষই বিচার করতে হবে। এ অধ্যায়ে আমাদের এই তথ্যই বিচার্য।

আমাদের তৃতীয় স্বীকার্য : ভ্রাম্যমাণ আলোকশ্মির যে কোনো দুটি অংশের মধ্যবর্তী অন্তর শূন্য (zero)। এই স্বীকার্যের একটি সুবিধা এই যে, শুধুমাত্র স্বল্প দূরত্বের জন্য একথা বলার কোনো প্রয়োজন নেই। অন্তরের প্রতিটি ক্ষুদ্র অংশই যদি শূন্য হয় তাহলে তাদের যোগফলও হবে শূন্য সুতরাং সেই আলোকরশ্মির দূরস্থিত অংশগুলিরও অন্তর শূন্য হবে। এই স্বীকার্য অনুসারে আলোকরশ্মির গতিপথও ধরাকৃতি। সুতরাং এখন স্থান-কালে ধরাকৃতি আবিষ্কারের দুটি প্রয়োেগজ (empirical) পদ্ধতি আমাদের রয়েছে : আলোকরশ্মি এবং অবাধে চলমান বস্তুপিণ্ড। অবাধে চলমান বস্তুপিণ্ডগুলির ভিতরে রয়েছে সেগুলি, যেগুলি সামগ্রিক রূপে উপলব্ধিযোগ্যভাবে বিদ্যুৎচুম্বকীয় বল কিংবা ঊনপামাণবিক বলের প্রভাবাধীন নয়। অর্থাৎ সূর্য, তারকা, গ্রহ এবং উপগ্রহ এবং ভূপৃষ্ঠে পতনশীল বস্তুপিণ্ড-বিশেষ করে যখন শূন্যের ভিতর দিয়ে পড়েছে তখন। আপনি যখন পৃথিবীতে দাঁড়িয়ে তখন আপনি বিদ্যুৎচুম্বকীয় বলের প্রভাবাধীন : আপনার পায়ের সান্নিধ্যের ইলেকট্রন প্রোটনগুলি আপনার পায়ের উপর একটি বিকর্ষণ বল প্রয়োগ করছে। এই বল পৃথিবীর মহাকর্ষকে পরাস্ত করার পক্ষে পর্যাপ্ত। এই বলই আপনাকে পৃথিবীর ভিতর দিয়ে পড়ে যেতে বাধা দেয়। পৃথিবীকে দেখতে ঘন (solid) হলেও আসলে তার অধিকাংশই শূন্যস্থান।

—–
* ঈল (Eel)-লম্বা সাপের মতো দেখতে একরকম মাছ।