৭. স্থান-কাল অন্তর
এতক্ষণ আমরা বিচার করেছি বিশিষ্ট অপেক্ষবাদ। এ তত্ত্ব সম্পূর্ণ সমাধান করেছে নির্দিষ্ট নিশ্চিত বিশেষ একটি সমস্যা : দুটি বস্তুপিণ্ড যখন পরস্পর সাপেক্ষ সমরূপ আপেক্ষিক গতিসম্পন্ন তখন সাধারণ গতিবিদ্যা সংশ্লিষ্ট কিংবা বিদ্যুৎ ও চুম্বক সংশ্লিষ্ট পদার্থবিদ্যার সমস্ত বিধি দুটি বস্তুপিণ্ডেই নির্ভুলভাবে অভিন্ন পরীক্ষামূলক এই তথ্যের কারণ। এ ক্ষেত্রে ‘সমরূপ (uniform)’ গতির অর্থ সুষম (constant) ঋজুরেখ গতি। কিন্তু বিশিষ্ট তত্ত্ব একটি সমস্যার সমাধান করার সঙ্গে সঙ্গেই অন্য সমস্যার আভাস দেখা দিল। দুটি বস্তুপিণ্ডের গতি যদি সমরূপ না হয়? উদাহরণ : ধরুন একটি বস্তুপিণ্ড পৃথিবী এবং অন্যটি পতনশীল প্রস্তর । প্রস্তরের গতি ত্বরিত (accelerated)(১) অর্থাৎ এর পতনের গতি নিয়ত বর্ধমান। বিশিষ্ট অপেক্ষবাদে এমন কিছু নেই যার সাহায্যে আমরা বলতে পারি পাথরে অবস্থিত পর্যবেক্ষক এবং পৃথিবীতে অবস্থিত পর্যবেক্ষক এবং পৃথিবীতে অবস্থিত পর্যবেক্ষক সাপেক্ষ ভৌত পরিঘটনার বিধিগুলি অভিন্ন হবে। ব্যাপারটা আরো বেশি জটিল এইজন্য যে, বিস্তৃত অর্থে পৃথিবীটাই একটি পতনশীল বস্তুপিণ্ড, প্রতিমুহূর্তেই এর সূর্যের অভিমুখে ত্বরিত গতি রয়েছে।
এই গতির ফলেই পৃথিবী ঋতুরেখায় না গিয়ে সূর্যের চারপাশে আবর্তিত হয়। পৃথিবীভিত্তিক পরীক্ষা থেকে আমাদের পদার্থবিদ্যার জ্ঞান আহরিত সেইজন্য যে তত্ত্বে অনুমান করা হয় পর্যবেক্ষকের কোনো তরুণ নেই সে তত্ত্ব আমাদের সুতৃপ্ত করতে পারে না। ব্যাপক অপেক্ষবাদ এই বাধা দূর করেছে এবং এ তত্ত্ব পর্যবেক্ষকের ঋজু, বঙ্কিম, সমরূপ কিংবা ত্বরিত যে কোনোরকম গতিই অনুমোদন করে। এই বাধা দূর করতে গিয়ে আইনস্টাইন তার নতুন মহাকর্ষীয় বিধি সৃষ্টির দিকে অগ্রসর হয়েছেন। সে বিধি সম্পর্কে আলোচনাও আমরা অচিরে করব। কাজটা ছিল অসাধারণ শক্ত। এ কাজে তাঁর দশ বছর লেগেছে। বিশিষ্ট অপেক্ষবাদের শুরু ১৯০৫ সালে, আর ১৯১৫ সালে শুরু হয়েছে ব্যাপক অপেক্ষাবাদ।
সমরূপ গতির তুলনায় ত্বরিত গতি বিচার অনেক বেশি কঠিন। আমাদের সবার অভিজ্ঞতাতেই এ তথ্য স্বতঃপ্রতীয়মান। স্থির গতিতে চলমান একটি রেলগাড়িতে যাওয়ার সময় জানালা দিয়ে বাইরে না তাকানো পর্যন্ত গতি বোঝ যায় না। কিন্তু হঠাৎ ব্রেক কষলে আপনি সামনের দিকে হুমড়ি খেয়ে পড়েন। তখন বাইরের দিকে না তাকিয়েও আপনি বুঝতে পারেন একটা কিছু ঘটছে। লিফটেও তেমনি। যতক্ষণ পর্যন্ত লিফটটা সমরূপে চলমান থাকে ততক্ষণ পর্যন্ত ব্যাপারটা মনে হয় স্বাভাবিক কিন্তু শুরুর সময় আর থামবার সময় পেটের ভিতরটা যেন কেমন করে ওঠে। [দ্রুততর হওয়া এবং ধীরতর হওয়া এই দু’ক্ষেত্রেই আমরা গতিকে ত্বরিত’ (accelerated) বলি। ধীরতর হওয়ার সময় ত্বরণ অপরা (negative)]। জাহাজের কেবিনে একটা ওজন পরিত্যাগ করার ক্ষেত্রেও একই তথ্য প্রযোজ্য। যতক্ষণ পর্যন্ত জাহাজের গতি সমরূপ ততক্ষণ পর্যন্ত কেবিন সাপেক্ষ ওজনটার আচরণ এমন হবে যেন জাহাজটা স্থিরভাবে রয়েছে। ওজনটা যদি ছাতের মাঝখান থেকে পড়তে শুরু করে তাহলে সেটা পড়বে ঠিক মেঝের মাঝখানে। কিন্তু ত্বরণ থাকলে সবটাই বদলে যায়। জাহাজের গতি যদি দ্রুত বাড়তে থাকে তাহলে কেবিনের পর্যবেক্ষকের মনে হবে ওজনটা বক্ৰগতিতে পড়ছে; বক্রতার অভিমুখ জাহাজের পিছন দিকে। জাহাজের গতি যদি দ্রুত হ্রাস পেতে থাকে তাহলে বক্রতার অভিমুখ হবে জাহাজের সামনের দিকে। এ সব তথ্যই পরিচিত। এই জন্যই গ্যালিলিও এবং নিউটন ত্বরিতগতির নিজস্ব চরিত্রকে সমরূপ গতির চাইতে সম্পূর্ণ পৃথক বলে বিচার করেছিলেন। কিন্তু গতিকে আপেক্ষিক না ভেবে পরম (absolute) ভাবলেই শুধুমাত্র এ পার্থক্য রক্ষা করা যায়। সমস্ত গতিই যদি আপেক্ষিক হয় তাহলে পৃথিবী সাপেক্ষ লিটটা যে রকম ত্বরিত, লিফট সাপেক্ষ পৃথিবীটাও তেমনি ত্বরিত। তবুও মাটিতে যারা রয়েছে লিফ্টটা উপরে উঠবার সময় তাদের পেটে কোনো অনুভূতি হয় না। আমাদের সমস্যাটা কত কঠিন এ তথ্য তার একটা দৃষ্টান্ত। আসলে আধুনিক যুগের খুব কম পদার্থবিদ্যাবিদই পরম গতিতে বিশ্বাস করতেন, কিন্তু এ বিষয়ে নিউটনের বিশ্বাস গাণিতিক পদার্থবিদ্যার প্রযুক্তির অঙ্গীভূত ছিল এবং এ অনুমান। থেকে মুক্ত একটি প্রযুক্তিবিদ্যা পেতে হলে প্রয়োজন ছিল একটা পদ্ধতিগত বিপ্লব। এই বিপ্লব সুসম্পন্ন হয়েছে আইনস্টাইনের ব্যাপক অপেক্ষবাদে।
আইনস্টাইন যে নতুন ধারণাগুলি উপস্থিত করেছিলেন, সেগুলির ব্যাখ্যা কোথা থেকে শুরু করব সেটা অনেকখানি নির্ভর করে আমাদের ইচ্ছার উপর, কিন্তু আমাদের পক্ষে বোধহয় সবচাইতে ভাল হবে অন্তর’ (interval) সম্পর্কীয় কল্পন দিয়ে শুরু করা। এ কল্পন বিশিষ্ট অপেক্ষবাদে যেভাবে উপস্থাপিত হয়েছে। সেটা আসলে স্থানিক এবং কালিক দূরত্ব সম্পর্কীয় চিরায়ত চিন্তনের সাধারণীকরণ, কিন্তু এ সাধারণীকরণের আরো বিস্তার প্রয়োজন। যাই হোক– প্রথম আমাদের দরকার খানিকটা ইতিহাস ব্যাখ্যা করা। সেইজন্য আমাদের প্রয়োজন অতীতে পিথাগোরাস (Pythagoras) পর্যন্ত যাওয়া।
ইতিহাসের বহু চরিত্রের মতো পিথাগোরাস নামে কোনো লোকের অস্তিত্ব হয়তো ছিল না। স্ত্রীই হোন আর পুরুষই হোন পিথাগোরাস একটি অর্ধ পৌরাণিক চরিত্র। তিনি গণিতশাস্ত্র এবং পৌরোহিত্যবিদ্যা এক অনিশ্চিত অনুপাতে মিশিয়েছিলেন। যাই হোক আমি অনুমান করব পিথাগোরাস নামক ব্যক্তির অস্তিত্ব ছিল এবং তাঁর নামে প্রচলিত উপপাদ্য ঐ নামের কেউ আবিষ্কার করেছিলেন। পিথাগোরাস মোটামুটি কনফুসিয়াস এবং বুদ্ধের সমসাময়িক। তিনি একটি ধর্মসম্প্রদায় স্থাপন করেছিলেন। সে সম্প্রদায়ের ধারণা ছিল সিম খাওয়া মহাপাপ। তাছাড়া তিনি একটি গাণিতিক গোষ্ঠী স্থাপন করেছিলেন। সমকোণী ত্রিভুজে ছিল তাদের বিশেষ আকর্ষণ। পিথাগোরাসের উপপাদ্য-এর (ইউক্লিডের ৪৭ তম প্রতিজ্ঞা) বক্তব্য : একটি সমকোণী ত্রিভুজের দুটি ক্ষুদ্রতর বাহুর বর্গের যোগফল সমকোণের বিপরীত বাহুর বর্গের তুল্য (equal সমান) সমগ্র গণিতশাস্ত্রে কোনো প্রতিজ্ঞার (proposition) ইতিহাসই এরকম গৌরবান্বিত নয়। তরুণ বয়সে আমরা সবাই এ প্রতিজ্ঞা প্রমাণ করতে শিখেছি। সে ‘প্রমাণ’ কিছুই ‘প্রমাণ করেনি সে কথা সত্য প্রমাণের একমাত্র পথ পরীক্ষা। তাছাড়া ঘটনা হল, প্রতিজ্ঞাটা সম্পূর্ণ সত্য নয়– আসন্ন (approximate) সত্য মাত্র। কিন্তু সম্পূর্ণ জ্যামিতি এবং পরবর্তীকালে পদার্থবিদ্যা, পারস্পরিক সাধারণীকরণের সাহায্যে এই প্রতিজ্ঞা থেকে আহরণ করা হয়েছে। এগুলির একটি হল ব্যাপক অপেক্ষবাদ।
যতদূর সম্ভব পিথাগোরাসের উপপাদ্য স্বতত মিশরীয়দের কার্যক্ষেত্রে চলিত একটি নিয়মের (rule of thumb) সাধারণকরণ। মিশরে বহুদিন ধরে জানা ছিল: যে ত্রিভুজের বাহু দৈর্ঘ্যে ৩, ৪ এবং ৫ একক সে ত্রিভুজ সমকোণী। মিশরীয়রা ব্যবহারিক কার্যক্ষেত্রে মাপার জন্য এই জ্ঞান প্রয়োগ করতেন। ত্রিভুজের বাহুগুলি যদি ৩, ৪ এবং ৫ ইঞ্চি হয় তাহলে সেগুলির উপরের বর্গের বর্গফল হবে যথাক্রমে ৯, ১৬ এবং ২৫ বর্গইঞ্চি এবং ৯ এবং ১৬ যোগ দিলে হয় ২৫। লিখবার সময় তিনের তিনগুণ ৩২, চারের চারগুণ ৪২, পঁচের পাঁচগুণ ৫২, সুতরাং আমরা পাই:
৩^২+ ৪^২=৫^২
অনুমান করা হয় যে ত্রিভুজের বাহুগুলি ৩, ৪ এবং ৫–সে ত্রিভুজে একটি সমকোণ থাকে এ তথ্য পিথাগোরাস মিশরীয়দের কাছ থেকে শিখেছিলেন এবং তারপর ব্যাপারটা লক্ষ্য করেছিলেন। পিথাগোরাস দেখলেন এ তথ্যের সাধারণীকরণ সম্ভব এবং এইভাবে এলেন তাঁর বিখ্যাত উপপাদ্যে : একটি সমকোণী ত্রিভুজে, সমকোণের বিপরীত বাহুর উপরে গঠিত সমচতুর্ভুজ অন্য দুটি বাহুর উপরে গঠিত সমচতুর্ভুজের যোগফলের সমান।
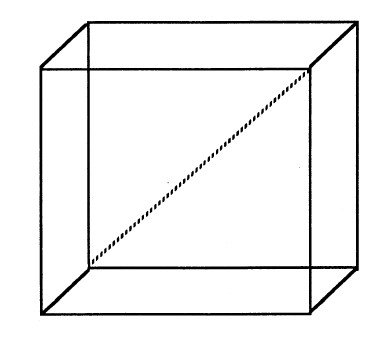
ত্রিমাত্রিকও ব্যাপারটা একই : যদি সমকোণী কঠিন ঘনক বিচার করেন তাহলে কর্ণের (diagonal) উপরের সমচতুর্ভুজ (চিত্রের বিচ্ছিন্ন রেখা) এবং তিনটি পার্শ্বের উপরের সমচতুর্ভুজের যোগফল সমান।
এ ব্যাপারে প্রাচীনেরা এই পর্যন্ত পৌঁছেছিলেন।
এর পরের গুরুত্বপূর্ণ ধাপ এসেছে দেকার্তের (Descartes) কাছ থেকে। পিথাগোরাসের উপপাদ্যকে তিনি তাঁর বৈশ্লেষিক জ্যামিতিক পদ্ধতির ভিত্তি করেছিলেন। ধরুন আপনি সুসম্বন্ধভাবে (systematically) একটি সমতলের সর্বস্থানের মানচিত্র আঁকতে চান”। আমরা ধরে নেব জায়গটা এত ছোট যে পৃথিবীর বর্তুলাকৃতি অগ্রাহ্য করা সম্ভব। আমরা অনুমান করব আপনি সমতলের মাঝখানে বাস করেন। একটি জায়গায় অবস্থানের বিবরণ দেওয়ার সহজতম একটি উপায় হল এই কথা বলা : আমার বাড়ি থেকে প্রথমে পূর্ব দিকে এতটা দূরত্ব যাবেন তারপর যাবেন উত্তরে এতটা দূরত্ব। (কিংবা প্রথম ক্ষেত্রে এটা হতে পারে পশ্চিম এবং দ্বিতীয় ক্ষেত্রে হতে পারে দক্ষিণ)। এইভাবে জায়গার অবস্থান আপনি নির্ভুলভাবে জানতে পারছেন। আমেরিকার আয়তক্ষেত্রাকার (rectangu lar) শহরগুলিতে এই পদ্ধতি গ্রহণ করাই স্বাভাবিক : নিউ ইয়র্কে আপনাকে বলবে : এই কটা ব্লক (block) পূর্বে (কিংবা পশ্চিমে) যান তারপর উত্তরে (কিংবা দক্ষিণে) যান এই কটা ব্লক। পূর্বে আপনার যতটা দূরত্ব যেতে হচ্ছে তার নাম X এবং উত্তরে যতটা দূরত্ব আপনাকে যেতে হচ্ছে তার নাম Y। আপনার যদি পশ্চিমে যেতে হয় তাহলে X অপরা (negative) আর যদি দক্ষিণে যেতে হয় তাহলে Y অপরা। 0 হোক আপনার আরম্ভ বিন্দু (উৎপত্তি), পূর্বদিকে যাওয়া দূরত্ব হোক OM এবং উত্তর দিকে যাওয়া দূরত্ব হোক MP। আপনি যখন P-এতে পৌঁছেছেন তখন আপনি প্রত্যক্ষ রেখায় (direct lines) আপনার বাড়ি থেকে কত দূরে? এর উত্তর দেয় পিথাগোরাসের উপপাদ্য।
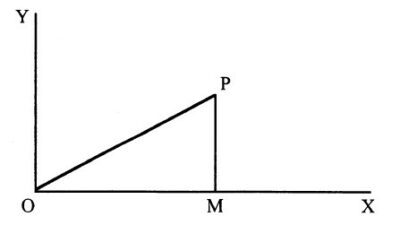
OP-এর উপরে বর্গ MP এবং OM-এর উপরের বর্গের যোগফলের সমান। OM যদি চার মাইল হয় এবং MP যদি তিন মাইল হয় তাহলে OP পাঁচ মাইল। OM যদি বারো মাইল হয় এবং MP যদি পাঁচ মাইল হয় তাহলে OP তেরো মাইল। তার কারণ ১২২… ৫২… ১৩২। সুতরাং আপনি যদি দেকার্তের মানচিত্রাঙ্কন পদ্ধতি গ্রহণ করেন তাহলে স্থান থেকে স্থানান্তরে দূরত্ব নির্ধারণের জন্য পিথাগোরাসের উপপাদ্য অপরিহার্য। ত্রিমাত্রিকে (in three dimensions) ব্যাপারটা একেবারেই এক রকম। আপনি যদি শুধুমাত্র সমতলে স্থান স্থির না করে, উপরে আবদ্ধ বেলুনের অবস্থান নির্দিষ্ট করতে চান তাহলে আপনাকে তৃতীয় একটি রাশি যোগ করতে হবে : অর্থাৎ বেলুন যে উচ্চতায় থাকবে। উচ্চতা যদি z হয়, বেলুন থেকে ০ এর প্রত্যক্ষ (direct) দূরত্ব যদি r হয় তাহলে আপনি পাবেন–
r^2 = x^2 + y^2 + z^2
x, y এবং z জানা থাকলে এ থেকে আপনি r গণনা করতে পারবেন। উদাহরণ : আপনার যদি বেলুনের কাছে যেতে বারো মাইল পুর্বদিকে যাওয়ার পর চার মাইল উত্তরে গিয়ে তিন মাইল উপরে যেতে হয় তাহলে বেলুন থেকে ঋজুরেখায় আপনার দূরত্ব হবে তেরো মাইল। কারণ, ১২ x ১২ = ১৪৪, ৪ X ৪ = ১৬, ৩ x ৩ = ৯, ১৪৪ + ১৬+৯ = ১৬৯ = ১৩ x ১৩।
কিন্তু ধরুন ভূ-পৃষ্ঠের সামান্য অংশ না নিয়ে আপনি সম্পূর্ণ পৃথিবীর মানচিত্র আঁকবার কথা ভাবছেন। ভূ-পৃষ্ঠের সামান্য অংশকে সমতল ভাবা যেতে পারে। কিন্তু সমতল কাগজে পৃথিবীর নির্ভুল মানচিত্র আঁকা অসম্ভব। সবটাই মানক (scale) অনুসারে করা যায় এই জন্য একটা গোলক (globe) নির্ভুল হতে পারে কিন্তু সমতল মানচিত্র নির্ভুল হতে পারে না। ব্যবহারিক অসুবিধার কথা আমি বলছি না, আমি বলছি তাত্ত্বিক দিক দিয়ে ব্যাপারটা অসম্ভব। উদাহরণ : গ্রিনউইচ মধ্যরেখার (meridian of Greenwich) উত্তরাংশ এবং পশ্চিম দ্রাঘিমার নবতিতম মধ্যরেখা আর অন্তবর্তী বিষুবরেখার অংশ মিলিয়ে একটি ত্রিভুজ সৃষ্টি করে। এই ত্রিভুজের প্রত্যেকটি বাহু সমান এবং কোণগুলির প্রত্যেকটিই এক একটি সমকোণ। একটি সমতলে এ ধরনের ত্রিভুজ অসম্ভব। অন্যদিকে আবার সমতলে একটি বর্গক্ষেত্র (square) সৃষ্টি সম্ভব কিন্তু গোলকের উপর সম্ভব নয়। অনুমান করা যাক পৃথিবীপৃষ্ঠে আপনি চেষ্টা করছেন : পশ্চিমে একশ’ মাইল গেলেন, তারপর উত্তরে গেলেন একশ’ মাইল, পূবদিকে একশ মাইল তারপর, এবং তারপর গেলেন একশ’ মাইল দক্ষিণে। আপনি ভাবতে পারেন এর ফলে একটি বর্গক্ষেত্র (square) তৈরি হবে। আসলে কিন্তু তা হবে না। কারণ যাত্রাশেষে আপনি আরম্ভ বিন্দুতে পৌঁছাবেন না। সময় না থাকলে এই পরীক্ষার সাহায্যে আপনি নিজেকে বিশ্বাস করাতে পারেন; সময় না থাকলে আপনি সহজেই বুঝতে পারেন– এইরকমই হওয়ার কথা। আপনি যখন মেরুর নিকটতর তখন একশ’ মাইল যেতে বিষুবরেখার নিকটতর অবস্থার তুলনায় আপনাকে অনেক বেশি দ্রাঘিমা (more longitude) অতিক্রম করতে হবে। সুতরাং একশ’ মাইল পূর্বদিকে গেলে (আপনার অবস্থান যদি উত্তর গোলার্ধে হয়) আপনি যে বিন্দুতে পৌঁছাবেন সে বিন্দু যাত্রারম্ভ বিন্দুর তুলনায় অনেক বেশি পূর্বদিকে; এরপর আপনি যখন সঠিক দক্ষিণে হাঁটছেন তখন আপনার অবস্থান আরম্ভ বিন্দুর তুলনায় আরো পূর্বদিকে এবং যাত্রা যেখানে শেষ করবেন সে স্থান আপনার আরম্ভ বিন্দু নয়। আর একটি উদাহরণ : অনুমান করা যাক আপনি শুরু করছেন গ্রিনউইচ মধ্যরেখার চার হাজার মাইল পূর্বদিকে বিষুবরেখার উপরে। তারপর আপনি চললেন গ্রিনউইচের ভিতর দিয়ে ঐ মধ্যরেখা বরাবর উত্তরদিকে চার হাজার মাইল এবং শেটল্যান্ড দ্বীপপুঞ্জের কাছাকাছি গেলেন। তারপর আপনি গেলেন পূর্বদিকে চার হাজার মাইল এবং সেখান থেকে গেলেন দক্ষিণে চার হাজার মাইল। এর ফলে আপনি বিষুবরেখার যে বিন্দুতে পৌঁছাবেন সে বিন্দু আপনার যাত্রারম্ভ বিন্দু থেকে আরো চার হাজার মাইল পূর্বদিকে।
আসলে এতক্ষণ পর্যন্ত আমরা যা বলেছি সেটা ঠিক ন্যায্য কথা নয়। তার কারণ একমাত্র বিষুবরেখার উপরে ছাড়া কোথাও একস্থান থেকে সঠিক পূর্বদিকে অন্যস্থানে যাওয়ার হ্রস্বতম পথ সঠিক পূর্বমুখী নয়। নিউইয়র্ক থেকে লিসবন প্রায় সঠিক পূর্বদিকে। জাহাজে (ধরুন) নিউইয়র্ক থেকে লিসবন যেতে গেলে জাহাজটা যাত্রা শুরু করে খানিকটা উত্তর দিকে গিয়ে। জাহাজটা চলে বৃহৎ বৃত্তে অর্থাৎ এমন বৃত্ত পৃথিবীর। কেন্দ্রেই যার নিজস্ব কেন্দ্র। এটাই ভূ-পৃষ্ঠে অঙ্কনসাধ্য ঋজুরেখার নিকটতম। বিষুবরেখা তথা দ্রাঘিমার মধ্যরেখাগুলি বৃহৎ কিন্তু অক্ষাংশের (latitude) অন্য সমান্তরালগুলি নয়। সুতরাং আমাদের অনুমান করা উচিত ছিল শেটল্যান্ড দ্বীপপুঞ্জে পৌঁছানোর সময় আপনার চার হাজার মাইল ভ্রমণ করা হয়েছে তবে সঠিক পুর্বদিকে নয়, আপনি ভ্রমণ করেছেন এমন একটি বৃত্ত বরাবর যে বৃত্ত আপনাকে শেটল্যান্ড দ্বীপপুঞ্জের সঠিক পুর্বদিকে নিয়ে এসেছে। এ তথ্য কিন্তু আমাদের এই সিদ্ধান্তকেই দৃঢ়তর করে : আপনি আগের তুলনায় আপনার প্রারম্ভ বিন্দুর চাইতে আরো বেশি পূর্বদিকে যাত্রা শেষ করবেন।
সমতলের উপরের জ্যামিতি এবং গোলকের উপরের জ্যামিতিতে পার্থক্য কি? আপনি পৃথিবীর উপর যদি একটি ত্রিভুজ তৈরি করেন এবং তার বাহুগুলি যদি বৃহৎ বৃত্ত হয় তাহলে আপনি দেখতে পাবেন ত্রিভুজের কোণগুলির যোগফল দুই সমকোণ নয়। যোগফল তার চাইতে কিছু বেশি। দুই সমকোণের চাইতে আধিক্যের পরিমাণ ত্রিভুজের আকারের আনুপাতিক। ঘাসের উপর সুতো দিয়ে বানানো ত্রিভুজ কিংবা ঐরকম ছোট একটি ত্রিভুজে, এমন কি, পরস্পর দৃশ্যমান তিনটি জাহাজ দিয়ে তৈরি ত্রিভুজের কোণগুলি যোগ দিলেও যোগফল দুই সমকোণের বেশি হবে। কিন্তু সে আধিক্য এত কম যে পার্থক্যটা আপনি ধরতে পারবেন না। কিন্তু আপনি যদি বিষুবরেখা, গ্রিনউইচ মধ্যরেখা এবং নবতিতম মধ্যরেখা দিয়ে ত্রিভুজ তৈরি করেন তাহলে কোণগুলির যোগফল হবে তিন সমকোণ। আপনি এমন ত্রিভুজও পেতে পারেন যার যোগফল হতে পারে ছয় সমকোণ পর্যন্ত যা কিছু। এগুলি আপনি ভূ-পৃষ্ঠে মাপনের সাহায্যেই আবিষ্কার করতে পারেন তার জন্য পৃথিবী বহির্ভূত স্থানে (space) অবস্থিত অন্য কিছু বিচার করার প্রয়োজন নেই।
গোলক পৃষ্ঠের দূরত্বের ব্যাপারে পিথাগোরাসের উপপাদ্যও বিফল হবে। পৃথিবীতে আবদ্ধ পথিকের দৃষ্টিভঙ্গি থেকে দুটি স্থানের দূরত্ব হল তাদের বৃহৎ বৃত্ত দূরত্ব অর্থাৎ ভূ-পৃষ্ঠ ত্যাগ না করা পর্যন্ত ক্ষুদ্রতম দূরত্ব এটাই। অনুমান করা যাক। বৃহৎ বৃত্তগুলির এমন তিনটি টুকরো আপনি নিয়েছেন যা দিয়ে একটা ত্রিভুজ বানানো সম্ভব। আরো অনুমান করা যাক তাদের ভিতরে একটি অন্য একটি সাপেক্ষ সমকোণে অবস্থিত। নিশ্চিতভাবে বলতে হলে একটা হোক বিষুবরেখা, আর অন্যটি হোক গ্রিনউইচ মধ্যরেখার বিষুবরেখা থেকে উত্তরগামী একটি অংশ। অনুমান করা যাক আপনি বিষুবরেখা বরাবর তিন হাজার মাইল গিয়েছেন তারপর সঠিক উত্তরে গিয়েছেন চার হাজার মাইল, তাহলে একটি বৃহৎ বৃত্ত বরাবর দূরত্ব হিসাব করলে আপনি আরম্ভ বিন্দু থেকে কতদূরে থাকবেন? আগে আমরা দেখেছি এরোপ্লেনে থাকলে আপনার দূরত্ব হবে পাঁচ হাজার মাইল । আসলে কিন্তু আপনার বৃহৎ বৃত্ত দূরত্ব এর চাইতে অনেক কম হবে। গোলকপৃষ্ঠে একটি সমকোণী ত্রিভুজে সমকোণের বিপরীত বাহুর উপরের বর্গ অন্য দুটি বাহুর উপরের বর্গের যোগফলের চাইতে কম।
গোলক পৃষ্ঠের জ্যামিতি এবং সমতলের জ্যামিতির ভিতরে এই পার্থক্যগুলি স্বকীয় (intrinsic) অর্থাৎ যে পৃষ্ঠে (surface) আপনি বসবাস করেন সেই পৃষ্ঠ গোলক তুল্য না সমতল তুল্য, জ্যামিতির এই পার্থক্যগুলি সে তথ্য আবিষ্কার করার ক্ষমতা আপনাকে দান করে। তার জন্য পৃষ্ঠ বহির্ভুত কিছু বিচারের প্রয়োজন হয় না। এই বিচারগুলি পরের গুরুত্বপূর্ণ পদক্ষেপের পথিকৃৎ। এ কাজ করেছিলেন গাউস (Gauss)। তাঁর গৌরবময় কর্মজীবন ‘দেড়শ’ বছর আগেকার । গাউস তল (surface) সম্পর্কীয় তত্ত্বে মনোনিবেশ করেছিলেন। তিনি দেখিয়েছিলেন স্বতত বিভিন্ন তলগুলি মাপনের সাহায্যে এবং তলের বাইরে না গিয়ে এ তত্ত্বের বিকাশ কি করে সম্ভব স্থানে একটি বিন্দুর অবস্থান স্থির করার জন্য আমাদের তিনটি মাপন প্রয়োজন কিন্তু পৃষ্ঠতলে (surface) একটি বিন্দুর অবস্থান স্থির করার জন্য আমাদের প্রয়োজন দুটি। উদাহরণ : অক্ষাংশ এবং দ্রাঘিমা জানা থাকলে পৃথিবীর পৃষ্ঠতলে একটি বিন্দুর অবস্থান স্থির করা যায়।
গাউস দেখেছিলেন, মাপনের যে পদ্ধতিই আপনি গ্রহণ করুন না কেন এবং তলের চরিত্র যাই হোক না কেন, দুটি বিন্দুর অন্তবর্তী দূরত্ব মাপন সম্ভব। অবশ্য সে দূরত্ব যদি খুব বেশি না হয় এবং বিন্দুগুলির অবস্থান নির্দেশক রাশিগুলি যদি জানা থাকে। দূরত্বের সঙ্কেত পিথাগোরাসের সঙ্কেতের সাধারণীকরণ। এ সঙ্কেত আপনাকে বলবে : যে মাপনরাশিগুলি বিন্দুগুলির অবস্থান নির্দেশক সেগুলির পার্থক্যের বর্গের বাগ্বিধিতে দূরত্বের বর্গ এবং বলবে এই দুটি রাশির গুণফল। এই সঙ্কেত জানা থাকলে আপনি তলের স্বকীয় ধর্মের সবটাই আবিষ্কার করতে পারেন অর্থাৎ জানতে পারবেন সেই ধর্মগুলি যে ধর্ম তল বহির্ভূত কোনো বিন্দুর সঙ্গে তার সম্পর্কের উপর নির্ভরশীল নয়। উদাহরণ : আপনি আবিষ্কার করতে পারবেন একটি ত্রিভুজের কোণগুলির যোগফলের সমষ্টি দুই সমকোণ কিংবা বেশি কিংবা কম অথবা কোনো ক্ষেত্রে কম কোনো ক্ষেত্রে বেশি কিনা।
কিন্তু যখন আমরা ‘ত্রিভুজের কথা বলি তখন আমরা কি বোঝাতে চাইছি সেটা ব্যাখ্যা করতেই হবে। কারণ অধিকাংশ তলেই কোনো ঋজুরেখা নেই। একটি গোলকের বেলায় আমরা ঋজুরেখার বদলে বৃহৎ বৃত্ত প্রতিস্থাপন করব। বৃহৎ বৃত্তই ঋজুরেখার নিকটতম। এমনিতে ঋজুরেখার পরিবর্তে আমরা গ্রহণ করব সেই সমস্ত রেখা যে রেখা স্থান থেকে স্থানান্তরের হ্রস্বতম পথ। এই জাতীয় রেখার নাম ধরাকৃতি (geodesics)। বৃহৎ বৃত্তই (great circles) ভূ-পৃষ্ঠের ধরাকৃতি। আপনি যদি পৃষ্ঠ (surface) ত্যাগ করতে অসমর্থ হন তাহলে এক বিন্দু থেকে অন্য বিন্দুতে যাওয়ার হ্রস্বতম পথ এগুলিই। একটি পৃষ্ঠের নিজস্ব (intrin sic) জ্যামিতিতে এগুলি ঋজুরেখার স্থান গ্রহণ করে। যখন আমরা প্রশ্ন করি, একটি ত্রিভুজের তিনটি কোণের যোগফল দুই সমকোণ কিনা তখন আমরা এমন ত্রিভুজ বোঝাতে চাই যার বাহুগুলি ধরাকৃতি। এবং যখন আমরা দুটি বিন্দুর অন্তবর্তী দূরত্বের কথা বলি তখন আমরা বোঝাতে চাই ধরাকৃতি বরাবর দূরত্ব।
আমাদের সাধারণীকরণে পরের ধাপ একটু কঠিন : সে ধাপ হল অনিউক্লিডীয় জ্যামিতিতে উত্তরণ (transition)। আমরা এমন বিশ্বে বাস করি সেখানে স্থান ত্রিমাত্রিক (three dimensions)। স্থান সম্পর্কে আমাদের অভিজ্ঞতালব্দ জ্ঞানের ভিত্তি স্বল্প দূরত্ব এবং ক্ষুদ্র কোণ মাপন। (স্বল্প দূরত্ব বলতে আমি বোঝাতে চাই সেই দূরত্বকে যে দূরত্ব জ্যোতির্বিজ্ঞানে ব্যবহৃত দূরত্বের তুলনায় স্বল্প। এই অর্থে পৃথিবীর সমস্ত দূরত্বই স্বল্প)। আগে ভাবা হতো স্থান ইউক্লিডীয় : এ তথ্য পূর্বত সিদ্ধ (a priori)। উদাহরণ : একটি ত্রিভুজের কোণগুলির যোগফল দুই সমকোণ। কিন্তু বোঝা গেল যুক্তি দিয়ে এ তথ্য প্রমাণ করা যায় না। প্রয়োজনে এ তথ্য জানতে হবে মাপনের ফলরূপে। আইনস্টাইনের আগে চিন্তা করা হতো প্রাপ্তিযোগ্য নির্ভুলতা সাপেক্ষ মাপন ইউক্লিডীয় জ্যামিতির সত্যতা প্রমাণ করে। এরকম চিন্তা এখন অচল। যাকে বলা যেতে পারে স্বাভাবিক কৌশল (natural artifice) তার সাহায্যে পৃথিবীর মতো একটি ক্ষুদ্র এলাকার সর্বত্র ইউক্লিডীয় জ্যামিতিকে সত্য মনে করানো যেতে পারে। কিন্তু মহাকর্ষ ব্যাখ্যা করতে গিয়ে আইনস্টাইন এই দৃষ্টিভঙ্গিতে পৌঁছালেন যে, পদার্থ যেখানে রয়েছে সেখানকার বিরাট বিরাট অঞ্চলে স্থানকে ইউক্লিডীয় ভাবা চলে না। এর কারণ জানার প্রয়োজন আমাদের এর পরে হবে। এখন আমাদের আলোচ্য বিষয় গাউসীয় গবেষণার সাধারণীকরণের ফলে অনিউক্লিডীয় জ্যামিতি সৃষ্টির পদ্ধতি।
উদাহরণ : গোলক পৃষ্ঠে যে পরিস্থিতি আমরা দেখতে পাই ত্রিমাত্রিক স্থানে সেই একই পরিস্থিতি না পাওয়ার কোনো কারণ নেই। এমন হতে পারে, ত্রিভুজের তিনটি কোণের যোগফল সব সময়ই দুই সমকোণের বেশি হবে এবং বৃদ্ধিটা হবে সবসমই ত্রিভুজের আকারের আনুপাতিক। এমন হতে পারে, গোলকপৃষ্ঠ সম্পর্কে আমাদের যে সঙ্কেত রয়েছে তার অনুরূপ কোনো সঙ্কেতের সাহায্যে দুটি বিন্দুর দূরত্ব প্রকাশিত হবে। এরকম ঘটে কিনা সেটা আবিষ্কৃত হতে পারে, গোলকপৃষ্ঠ সম্পর্কে আমাদের যে সঙ্কেত রয়েছে তার অনুরূপ কোনো সঙ্কেতের সাহায্যে দুটি বিন্দুর দূরত্ব প্রকাশিত হবে। এরকম ঘটে কিনা সেটা আবিষ্কৃত হতে পারে শুধুমাত্র যথাযথ মাপনের সাহায্যে। তবে সেক্ষেত্রে দুটির স্থলে তিনটি বড় সংখ্যা জড়িত থাকবে। এ জাতীয় সম্ভাবনার সংখ্যা অনন্ত।
রিম্যানের (Riemann) জ্যামিতির পেছনে যে প্রকল্প রয়েছে সেই সম্পর্কে (১৮৫৪) নামক গবেষণামূলক প্রবন্ধে যুক্তির এই ধারণা বিকাশ লাভ করেছিল। এ প্রবন্ধে তিনি তল সম্পর্কীয় গাউসের গবেষণাকে নানা ধরনের ত্রিমাত্রিক স্থান বিষয়ে প্রয়োগ করেছিলেন। তিনি দেখেছিলেন, এক রকমের একটা স্থান বিষয়ে মূলগত সমস্ত বৈশিষ্ট্যই ক্ষুদ্র দূরত্ব সম্পর্কীয় সঙ্কেত থেকে আহরণ করা সম্ভব। তিনি মনে করতেন : তিনটি অভিমুখের যে তিনটি ক্ষুদ্র দূরত্ব আপনাকে একেকটি বিন্দু থেকে স্বল্প দূরত্বে অবস্থিত অন্য বিন্দুতে পৌঁছে দেবে সেই দূরত্বগুলির সাহায্যে বিন্দু দুটির অন্তবর্তী দূরত্ব গণনা করা সম্ভব। উদাহরণ : যদি আপনার জানা থাকে একটি বিন্দু থেকে অন্য বিন্দুর দূরত্ব গণনা করার সামর্থ্য থাকা উচিত। এ গণনার নিয়ম হবে পিথাগোরাসের উপপাদ্যের বিস্তার (extension) অর্থাৎ দূরত্বের উপাদানগুলির (Component distances) বর্গের গুণিতকগুলি (multi ples) যোগ করে এবং সম্ভবত তাদের গুণফলগুলির গুণিতকগুলিকে সঙ্গে নিয়ে আপনি বলতে পারেন কি ধরনের স্থান নিয়ে আপনাকে কাজ করতে হবে। বিন্দুগুলির অবস্থান নির্ণয় করার জন্য আপনি কোন বিশেষ পদ্ধতি গ্রহণ করেছেন তার উপরে এই বৈশিষ্ট্যগুলি নির্ভর করে না।
অপেক্ষবাদের জন্য আমাদের যা দরকার সেটা পেতে হলে আমাদের আর একটি সাধারণীকরণ প্রয়োজন : বিন্দুগুলির অন্তর্বর্তী দূরত্বের স্থলে আমাদের প্রতিস্থাপন করতে হবে ঘটনাগুলির অন্তর’ (interval)। এ হল স্থান-কালের (space-time) পথিকৃৎ। বিশিষ্ট অপেক্ষবাদে আমরা আগেই দেখেছি ঘটনাগুলির অন্তর্বর্তী কালে আলোক যে দূরত্ব অতিক্রম করবে তার বর্গফল (square) থেকে ঘটনাগুলির দূরত্বের বর্গফল (square) বিয়োগ করলে অন্তরের (interval) বর্গফল পাওয়া যায়। ব্যাপক অপেক্ষবাদে অন্তরের এই বিশেষ অবয়ব আমরা অনুমান করি না। শুরুতে দূরত্ব বিষয়ে রিম্যান যা ব্যবহার করেছিলেন সেইরকম একটা সাধারণ অবয়ব আমরা অনুমান করি। তাছাড়া, আইনস্টাইন রিম্যানের মতো শুধুমাত্র নিকটবর্তী (neghbouring) ঘটনাবলী সম্পর্কেই সঙ্কেতটা অনুমান করেছিলেন (assumed), অর্থাৎ অনুমান করেছিলেন সেই ঘটনাগুলি সম্পর্কে যেগুলির অন্তর ক্ষুদ্র। এই প্রাথমিক মাননাগুলি অতিক্রম করে যা ঘটে সেগুলি নির্ভর করে বস্তুপিণ্ডগুলির বাস্তব গতি পর্যবেক্ষণের উপর। সে পদ্ধতি আমরা ব্যাখ্যা করব এর পরের অধ্যায়গুলিতে।
এতক্ষণ পর্যন্ত যে পদ্ধতির বিবরণ আমরা দিয়েছি এবার আমরা সেগুলির সংক্ষিপ্তসার করতে পারি এবং সেগুলি আবার বলতে পারি। ত্রিমাত্রিকে, একটি স্থির বিন্দু (আরম্ভ-origin) সাপেক্ষ একটি বিন্দুর অবস্থান নির্ণয় করা যায় তিনটি রাশি আরোপ করে (co-ordinate স্থানাঙ্ক) উদাহরণ : আপনার গৃহসাপেক্ষ একটি বেলুনের অবস্থান নির্ণয় করা যায় যদি আপনি জানেন সঠিক পূর্বে একটি বিশেষ দুরতে যাওয়ার পর উত্তরে আর একটি বিশেষ দূরত্ব অতিক্রম করে ঋজুভাবে সঠিক উর্ধ্বে আর একটি বিশেষ দূরত্ব অতিক্রম করলে আপনি সেই বেলুনে পৌঁছাকেন। এ ক্ষেত্রের মতো যেখানে পরস্পর সমকোণ সম্পর্কিত তিনটি দূরত্ব রয়েছে এবং যে ক্ষেত্রে আরম্ভ থেকে পরাক্রমে দূরত্বগুলি অতিক্রম করলে আপনি আলোচ্য বিন্দুতে পৌঁছে যাবেন। সে ক্ষেত্রে তিনটি স্থানাঙ্কের বর্গফল যোগ করলে প্রত্যক্ষ দূরত্বের বর্গফল পাওয়া যাবে। স্থান ইউক্লিডীয় কিংবা অনিউক্লিডীয় যাই হোক না কেন সর্বক্ষেত্রেই এটা পাওয়া যায় আরোপনযোগ্য একটি বিশেষ নিয়ম অনুসারে বর্গফলগুলির গুণিতক এবং স্থানাঙ্কগুলির গুণফল যোগের সাহায্যে। স্থানাঙ্কগুলি একটি বিন্দুর অবস্থান নির্দেশ করার মতো যে কোনো রাশিসমষ্টি হতে পারে তবে সন্নিকট বিন্দুগুলির স্থানাঙ্কও সন্নিকট রাশিসমষ্টিই হতে হবে। ব্যাপক অপেক্ষবাদে কালের জন্য আমরা একটি চতুর্থ স্থানাঙ্ক আরোপ করি। আমাদের সঙ্কেতে স্থানিক দূরত্বের বদলে আমরা পাই ‘অন্তর’। তাছাড়া শুধুমাত্র স্বল্প দূরত্বের ক্ষেত্রেই আমরা সঙ্কেতের ভ্রমহীনতা মাননা করি।
এবার আমরা আইনস্টাইনের মহাকর্ষীয় তত্ত্ব আলোচনা করার মতো অবস্থায় পৌঁছেছি।
——-
১. শুধু দ্রুতির (speed) বৃদ্ধিই নয়। গতি কিংবা অভিমুখের যে কোনো পরিবর্তনকেও ত্বরণ (accelera tion) বলা হয়। একমাত্র স্থির দ্রুতিতে ঋজুরেখ গতিকেই অত্বরিত (unaccelerated) গতি বলা হয়।
