৬. বিশিষ্ট অপেক্ষবাদ
বিদ্যুৎচুম্বকীয় তথ্য ব্যাখ্যা করার একটি পদ্ধতি রূপেই বিশিষ্ট অপেক্ষবাদের উদ্ভব। এই ইতিহাস বেশ অদ্ভুত। অষ্টাদশ শতাব্দী এবং উনবিংশ শতাব্দীর প্রথম দিকে বিদ্যুৎ বিষয়ক তত্ত্ব ছিল সম্পূর্ণভাবে নিউটনীয় তত্ত্বের সঙ্গে (Newtonian Analogy) সাদৃশ্যের প্রভাবাধীন। দুটি বৈদ্যুতিক আধান (electric charge) ভিন্নরূপের হলে অর্থাৎ একটি করা আধান (পজিটিভ আধান- Positive charge) এবং একটি অপরা আধান (নেগেটিভ আধান–Negative charge) হলে তারা পরস্পরকে আকর্ষণ করবে। আধান সমরূপের হলে তারা পরস্পরকে বিকর্ষণ করবে। মহাকর্ষের ক্ষেত্রে যেমন হয় তেমনি এর প্রতিটি ক্ষেত্রে বল বিপরীত বর্গে (inverse square) পরিবর্তী। ফ্যারাডের পূর্বে এই বলকে দূরের ক্রিয়ারূপে কল্পনা করা হতো। ফ্যারাডে কয়েকটি উল্লেখযোগ্য পরীক্ষার সাহায্যে অন্তবর্তী মাধ্যমের ক্রিয়া প্রদর্শন করেন। ফ্যারাডে গণিতবিদ্ ছিলেন না। ক্লার্ক-ম্যাক্সওয়েলই প্রথম ফ্যারাডের বৈজ্ঞানিক পরীক্ষালব্ধ ফলকে গাণিতিক রূপ দিয়েছেন। তাছাড়া আলোক একটি বিদ্যুৎচুম্বকীয় পরিঘটনা এবং বিদ্যুৎচুম্বকীয় তরঙ্গ দিয়ে আলোক গঠিত এই চিন্তনের ভিত্তি এসেছে ক্লার্ক-ম্যাক্সওয়েলের কাছ থেকে। সুতরাং বিদ্যুচ্চুম্বকীয় অভিক্রিয়া প্রেরণের মাধ্যম হিসাবে ইথারকে গ্রহণ করা যেত। ইথার আলোক প্রেরণের মাধ্যম এ অনুমান বহুকালের। বিদ্যুৎচুম্বকীয় তরঙ্গ তৈরি বিষয়ে হার্জ (Hertz)-এর পরীক্ষাগুলি ম্যাক্সওয়েলের আলোকতত্ত্বের নির্ভুলতা প্রমাণ করেছে। বেতার এবং রাডারের ভিত্তিও এই পরীক্ষাগুলি। এই পর্যন্ত রয়েছে আমাদের বিজয়োদ্ধত অগ্রগতির স্মারক (record of triumphant progress) তত্ত্ব। এবং বৈজ্ঞানিক পরীক্ষা পর্যায়ক্রমে এই অভিযানের নেতৃত্ব দিয়েছে। হার্জের পরীক্ষার সময় মনে হয়েছে ইথার দৃঢ়ভাবে প্রতিষ্ঠিত। প্রত্যক্ষ প্রমাণ সম্ভব নয় এই রকম যে কোনো বৈজ্ঞানিক প্রকল্পের (hypothesis) মতোই দৃঢ় ছিল ইথারের প্রতিষ্ঠা। কিন্তু আবিষ্কার হতে শুরু করল নতুন তথ্যমালা এবং ধীরে ধীরে পরিবর্তিত হল সম্পূর্ণ চিত্র।
সব জিনিসকে সন্তত (continuous) করার এই আন্দোলনকে সর্বোচ্চ স্তরে তুলে ধরেন হার্জ। ইথার ছিল সন্তত, ইথার তরঙ্গ ছিল সন্তত এবং আশা করা গিয়েছিল দেখা যাবে পদার্থের উপাদানেও রয়েছে ইথারের ভিতরের কয়েকটি সন্তত গঠন (structure)। কিন্তু তারপর আবিষ্কৃত হল পদার্থের পারমাণবিক গঠন এবং পরমাণুগুলির নিজস্ব বিবিক্ত (discrete) গঠন। বিশ্বাস ছিল পরমাণুগুলি ইলেকট্রন, প্রোটন এবং নিউট্রন দিয়ে গঠিত। ইলেকট্রন নির্দিষ্ট নিশ্চিত অপরা বৈদ্যুতিক আধান বহনকারী ক্ষুদ্র বস্তুকণা। প্রোটন বহন করে নির্দিষ্ট নিম্পিরা বৈদ্যুতিক আধান Positive electric charge)। নিউট্রনে কোনো বৈদ্যুতিক আধান নেই (ইলেকট্রনকে অপরা এবং প্রোটনকে পরা বলা হয়। উল্টোটা বলা হয় না শুধুমাত্র রীতির জন্য)। মনে হয়েছিল সম্ভবত ইলেকট্রন আর প্রোটনে আধান রূপে ছাড়া বিদ্যুৎ পাওয়া যায় না। সমস্ত ইলেকট্রনেই ঠিক একই অপরা বৈদ্যুতিক আধান রয়েছে এবং সমস্ত প্রোটনেই রয়েছে ঠিক সমান এবং বিপরীতধর্মী পরা বিদ্যুৎ আধান। এরপর আরো ঊনপারমাণবিক কণা (sub atomic particles) আবিষ্কৃত হয়। সমস্ত প্রোটনের ওজন অভিন্ন। এগুলি ইলেকট্রনের চাইতে প্রায় আঠার শত গুণ বেশি ভারী। সমস্ত নিউট্রনেরও ওজন ঠিক এক (exactly same weight) এগুলি প্রোটনের চাইতে সামান্য বেশি ভারী। মেসন অনেক ভিন্ন ভিন্ন রকমের রয়েছে। সেগুলির ওজন ইলেকট্রনের চাইতে বেশি কিন্তু প্রোটনের চাইতে কম। হাইপেরন প্রোটন কিংবা নিউট্রনের চাইতে ভারী।
কতগুলি কণায় বৈদ্যুতিক আধান রয়েছে আবার কতগুলিতে নেই। দেখা গিয়েছে পরা আধানযুক্ত কণাগুলির আধান একেবারেই পোটনের সমান আবার অপরা আধানযুক্ত কণাগুলির আধান যথাযথভাবে ইলেকট্রনের সমান। অথচ তাদের অন্যান্য ধর্মগুলি একেবারেই পৃথক। পজিট্রন (positron) নামে এক বস্তুকণা ব্যাপারটাকে আরো গোলমেলে করে দিয়েছে। এই বস্তুকণা এবং ইলেকট্রন অভিন্ন অথচ তার বৈদ্যুতিক আধান পরা, ইলেকট্রনের মতো অপরা নয়। পরীক্ষামূলকভাবে এমন কণা সৃষ্টি করা সম্ভব যা সর্ববিষয়ে প্রোটনের সঙ্গে অভিন্ন, শুধুমাত্র তার বৈদ্যুতিক আধান অপরা, এগুলির নাম এ্যান্টিপ্রোটন (antiproton)।
পদার্থের বিবিক্ত গঠন সম্পর্কীয় এই আবিষ্কারগুলিকে পরমাণুর বর্ণালীর উজ্জ্বল রেখাগুলির মতো অন্যান্য তথাকথিত কোয়ান্টাম পরিঘটনা আবিষ্কার থেকে পৃথক করা যায় না। মনে হয় যেখানেই যথেষ্ট নির্ভুল মাপন সম্ভব, প্রকৃতির সমস্ত পদ্ধতি সেখানেই মূলগত বিচ্ছিন্নতা প্রদর্শন করে।
পদার্থবিদ্যাকে এইভাবে হজম করতে হয়েছে নতুন নতুন তথ্য এবং মুখোমুখি হতে হয়েছে একাধিক নতুন সমস্যার। কোয়ান্টাম তত্ত্ব প্রায় আধুনিক অবয়বে বর্তমান রয়েছে ষাট বছর এবং বিশিষ্ট অপেক্ষবাদ রয়েছে আশি বছর কিন্তু এই দুটির সংযুক্ত বিষয়ে ত্রিশ বছর আগে পর্যন্ত বিশেষ কোনো অগ্রগতি হয়নি। সাম্প্রতিক বিকাশের ফলে কোয়ান্টাম তত্ত্ব বিশিষ্ট অপেক্ষবাদের সঙ্গে আরো সঙ্গতিপূর্ণ হয়েছে। এই অগ্রগতি ঊনপারমাণবিক কণা বুঝতে আমাদের অনেক সাহায্য করছে কিন্তু অনেক গুরুত্বপূর্ণ অসুবিধা রয়ে গিয়েছে।
কোয়ান্টাম তত্ত্ব ছাড়াও যে সমস্ত সমস্যা বিশিষ্ট অপেক্ষবাদ নিজ কৃতিত্বে (in its own right) সমাধান করেছে মিচেলসন-মর্লি পরীক্ষা তার একটি জাতিরূপ (tipefied)। ম্যাক্সওয়েলের বিদ্যুৎচুম্বকীয় তত্ত্বের সত্যতা মেনে নিলে ইথারের গতির কোনো আবিষ্কারযোগ্য ক্রিয়া থাকা উচিত ছিল কিন্তু কোনো কিছুই আসলে পাওয়া যায়নি। তাছাড়া অত্যন্ত দ্রুতগতিতে একটি বস্তুপিণ্ডের ভর বৃদ্ধি দেখা যায়; এ তথ্য পর্যবেক্ষণ করা হয়েছে। এই বৃদ্ধি আগের অধ্যায়ের চিত্রের OP-এর সঙ্গে MP-এর অনুপাতের সমান। এই ধরনের তথ্য জমতে থাকে এবং প্রয়োজন হয় এমন একটি তত্ত্বের যে তত্ত্ব এই সমস্ত তথ্যকে ব্যাখ্যা করতে পারে।
ম্যাক্সওয়েলের তত্ত্ব কতকগুলি সমীকরণে পরিণত হয়েছিল। সেগুলির নাম ‘ম্যাক্সওয়েল সমীকরণ। গত শতাব্দীতে পদার্থবিদ্যায় যে ক’টি বিপ্লব হয়েছে তার সবকটি অতিক্রম করেও ম্যাক্সওয়েল সমীকরণ বেঁচে আছে (remained stand ing)। আসলে এই সমীকরণগুলির গুরুত্ব এবং নিশ্চয়তা ক্রমশই বেড়েছে। এগুলির সপক্ষে ম্যাক্সওয়েলের যুক্তি ছিল এত দুর্বল যে এর নির্ভুলতার কৃতিত্ব প্রায় স্বজ্ঞার (intuition) উপরেই আরোপ করা উচিত সন্দেহ নেই। এই সমীকরণগুলির ভিত্তি ছিল পার্থিব গবেষণাগারে কৃত পরীক্ষা কিন্তু ইথারের ভিতর দিয়ে পৃথিবীর গতি অগ্রাহ্য করা যেতে পারে এই নীরব অনুমান ম্যাক্সওয়েল তত্ত্বে নিহিত ছিল। মিচেলসন-মর্লি পরীক্ষার মতো কতকগুলি ক্ষেত্রে মাপনযোগ্য ভুল ছাড়া এটা সম্ভব হওয়া উচিত ছিল না। কিন্তু দেখা গেল ব্যাপারটা সব সময়ই সম্ভব। পদার্থবিদ্যাবিদরা এক অদ্ভুত সঙ্কটে পড়েছিলেন : ম্যাক্সওয়েলের সমীকরণগুলি ছিল যতটা হওয়া উচিত তার চাইতেও নির্ভুল। আধুনিক পদার্থবিদ্যার শুরুতে একই রকম এক সঙ্কট ব্যাখ্যা করেছিলেন গ্যালিলিও। অধিকাংশ লোকেরই ধারণা একটি ওজনকে পড়তে দিলে সেটা পড়বে উল্লম্বভাবে (vertically)। কিন্তু আপনি যদি একটি চলমান জাহাজের কেবিনে এই পরীক্ষা করেন তাহলে কেবিন সাপেক্ষ ওজনটির পতন এমনভাবে হবে যেন জাহাজটি গতিহীন। উদাহরণ: ওজনটা ছাতের মাঝখান থেকে পড়তে শুরু করলে ঠিক মেঝের মাঝখানে এসে পড়বে। তীরের একজন পর্যবেক্ষক সাপেক্ষ পতন কিন্তু উল্লম্ব (vertical) নয় কারণ ওজনটা জাহাজের গতির অংশীদার। যতক্ষণ পর্যন্ত জাহাজের গতি অবিচলিত (steady) ততক্ষণ পর্যন্ত জাহাজের ভিতরের ঘটনাবলী এমন ভাবে হবে যেন জাহাজটি চলমান নয়। ব্যাপারটা কি করে হয় সে ব্যাখ্যা দিয়েছিলেন গ্যালিলিও। অ্যারিস্টটলের শিষ্যরা তাতে খুব অপমানিত বোধ করেছিলেন, বেজায় রেগে গিয়েছিলেন। গ্যালিলিও থেকে আহরিত প্রাচীন পদার্থবিদ্যা অনুসারে ঋজুরেখায় সমরূপ গতির কোনো আবিষ্কারযোগ্য অভিক্রিয়া (discoverable effects) নেই। আজকের দিনে আইনস্টাইনের আপেক্ষিকতা যে রকম বিস্ময়কর সে সময়ে গ্যালিলিওর আপেক্ষিকতাও (form of relativity) ছিল সেই রকম। বিশিষ্ট অপেক্ষবাদে আইনস্টাইনের কর্মপ্রচেষ্টা ছিল ইথারের ভিতর দিয়ে সমরূপ গতি দ্বারা কি করে বিদ্যুৎচুম্বকীয় পরিঘটনা অপ্রভাবিত থাকতে পারে সেটা দেখানো : অবশ্য ইথার বলে কিছু যদি থেকে থাকে তাহলে। এ সমস্যা ছিল আরো কঠিন। শুধুমাত্র গ্যালিলিওর নীতির ভিত্তিতে এ সমস্যার সমাধান সম্ভব ছিল না।
এ সমাধানের সত্যিকারের কঠিন প্রচেষ্টার প্রয়োজন ছিল কালিক সমস্যা বিষয়ে। প্রয়োজন ছিল বিশিষ্ট কাল সম্পর্কীয় ধারণা উপস্থাপন করা। এ বিষয়ে আমরা আগেই আলোচনা করেছি। আর প্রয়োজন ছিল এক ব্রহ্মাণ্ডীয় কাল সম্পর্কীয় প্রাচীন বিশ্বাস পরিত্যাগ করা। বিদ্যুৎচুম্বক পরিঘটনা সম্পর্কিত পরিমাণগত বিধি ম্যাক্সওয়েলের সমীকরণে প্রকাশিত। দেখা যায় সমস্ত পর্যবেক্ষক সাপেক্ষই এই সমীকরণগুলি সত্য পর্যবেক্ষকের প্রযুক্ত মাপনের সঙ্গে অন্য একজন পর্যবেক্ষকের প্রযুক্ত মাপনের পার্থক্য থাকবেই। তাদের আপেক্ষিক গতি সত্ত্বেও যদি তারা ঐ সমীকরণগুলির সত্যতা প্রমাণ করতে চায় তাহলে সে পার্থক্য নির্ণয় করা একটি প্রত্যক্ষ গাণিতিক সমস্যা মাত্র। এ সমস্যার উত্তর রয়েছে ‘লোরেঞ্জ রূপান্তরে। এটা একটা সঙ্কেতরূপে আবিষ্কার করেছিলেন লোরেঞ্জ (Lorentz) কিন্তু এর ব্যাখ্যা করেছিলেন আইনস্টাইন এবং একে বোধগম্য করেছিলেন তিনি।
একজন পর্যবেক্ষকের দূরত্ব এবং পরিব্যাপ্তিকাল আমাদের জানা থাকলে যার আপেক্ষিক গতি জানা আছে সেই রকম অন্য একজন পর্যবেক্ষকের প্রথমোক্ত পর্যবেক্ষকের দূরত্ব এবং পরিব্যাপ্তিকাল (Period of time) সম্পর্কে সম্ভাব্য অনুমান (estimate) প্রকাশ করেছে লোরেঞ্জ রূপান্তর।
আমরা অনুমান করতে পারি ঠিক পূর্বদিকগামী একটা রেলগাড়িতে আপনি রয়েছেন। যে স্টেশন থেকে আপনার যাত্রা শুরু সেই স্টেশনের ঘড়ি অনুসারে আপনার ভ্রমণকাল ‘t’। লাইনের উপরের লোকেদের মাপন অনুসারে আপনার যাত্রা বিন্দু থেকে x দূরত্বে এই মুহূর্তে একটা ঘটনা ঘটে–ধরুন লাইনে বাজ পড়ল। সব সময়ই আপনি গতি ‘V’ তে ভ্রমণ করছিলেন। প্রশ্নটা হল : আপনার বিচারে আপনার থেকে কতটা দূরে ঘটনাটা ঘটেছে বলে মনে হবে এবং রেলগাড়িতে অবস্থিত একজন পর্যবেক্ষকের দৃষ্টিভঙ্গিতে যদি আপনার ঘড়ি নির্ভুল অনুমান করা হয় তাহলে সেই ঘড়ি অনুসারে আপনার যাত্রা শুরুর কতক্ষণ পর ঘটনাটা ঘটেছে?
আমরা এই সমস্যার যে সমাধান করব সে সমাধানের কয়েকটি শর্ত পালন করতে হবে। সমাধান ফল এমন হতে হবে যে গতির প্রকার নির্বিশেষে সমস্ত পর্যবেক্ষক সাপেক্ষই আলোকের বেগ অভিন্ন হবে। তাছাড়া বিভিন্ন ভৌত পরিঘটনা, বিশেষ করে বিদ্যুচ্চুম্বকীয় পরিঘটনাগুলিকে, বিভিন্ন পর্যবেক্ষক সাপেক্ষ একই বিধি মানতে হবে। তাদের নিজস্ব গতির ফলে তাদের কাল এবং দূরত্ব মাপনে যতই ভিন্নতা প্রদর্শিত হোক না কেন ভৌত পরিঘটনাগুলিকে, বিশেষ করে বিদ্যুচ্চুম্বকীয় পরিঘটনাগুলিকে এই বিধি মানতে হবে। তাছাড়া মাপনের উপর নেই সমস্ত অভিক্রিয়াকে করতে হবে পারস্পরিক। অর্থাৎ আপনি যদি ট্রেনে থাকেন এবং আপনার গতি যদি ট্রেনের বাইরের সম্ভাব্য দূরত্ব সম্পর্কে আপনার অনুমানকে প্রভাবিত করে তাহলে যারা ট্রেনের বাইরে আছেন, ট্রেনের ভিতরকার সম্ভাব্য দূরত্ব সম্পর্কে তাদের অনুমানকেও ঠিক একই রকম প্রভাবিত হতে হবে। এই শর্তগুলি সমস্যার সমাধান নির্দেশ করার পক্ষে যথেষ্ট কিন্তু সমাধানের জন্য যে পরিমাণ গণিত প্রয়োজন এ পুস্তকে নিজেকে সে পরিমাণ গণিত ব্যবহারের অনুমতি আমি দিইনি।
ব্যাপারটা সাধারণভাবে আলোচনা করার আগে একটা উদাহরণ বিবেচনা করা যাক। অনুমান করা যাক আপনি দীর্ঘ ঋজুমুখী রেললাইনের উপরে একটা ট্রেনে রয়েছেন এবং আলোকের গতির পাঁচভাগের তিনভাগ গতিতে সঠিক পূর্ব দিকে চলেছেন। অনুমান করুন রেললাইনের দৈর্ঘ্য আপনি মেপেছেন এবং দেখেছেন গাড়িটা একশ’ গজ লম্বা। ধরুন– চলার পথে যারা আপনাকে এক পলক দেখতে পেয়েছে এবং তারা পর্যবেক্ষণের দক্ষতাপূর্ণ বৈজ্ঞানিক পদ্ধতির সাহায্যে আপনার গাড়ির দৈর্ঘ্য গণনা করতে পেরেছে। তাদের গণনা নির্ভুল হলে তারা দেখতে পাবে গাড়ির দৈর্ঘ্য আশি গজ, তাদের কাছে রেলগাড়ির গতির অভিমুখে গাড়ির ভিতরের প্রতিটি জিনিসেরই দৈর্ঘ্য আপনার যা মনে হয় তার চাইতে কম মনে হবে। আপনার দৃষ্টিতে খাওয়ার থালাগুলি সাধারণ বৃত্তাকার কিন্তু বাইরের লোকের দৃষ্টিতে সেগুলিকে মনে হবে ডিম্বাকৃতি। গাড়ির প্রস্থের অভিমুখের তুলনায় গাড়ির গতির অভিমুখে থালাগুলি মনে হবে চার-পঞ্চমাংশ চওড়া। সমস্তই আবার পারস্পরিক। ধরুন আপনি জানালা দিয়ে একটা মাছ ধরার ছিপ দেখতে পাচ্ছেন। যে লোকটি নিয়ে চলেছে সে দেখছে ছিপটা পনের গজ লম্বা। সেটা যদি খাড়া ভাবে (held upright) নেওয়া হয় তাহলে আপনি দেখবেন ওটা পনের ফুট লম্বা। ছিপটাকে যদি আনুভূমিকভাবে এবং রেললাইনের সঙ্গে সমকোণে বহন করা হয় (carried horizontally) তাহলেও ওটা পনের ফুট লম্বাই মনে হবে। কিন্তু রেললাইনের অভিমুখী হলে মনে হবে ছিপটা মোটে বারো ফুট লম্বা। যা দেখা যাচ্ছে তার বিবরণ দেওয়ার সময় আমি অনুমান করেছি। প্রত্যেকেই দর্শনানুপাতের সমুচিত বিচার করেছেন (due allowance for per spective)। তা সত্ত্বেও বাইরের লোকের বিচারে রেলগাড়ির প্রত্যেক জিনিসের দৈর্ঘ্যই গতির অভিমুখে শতকরা কুড়িভাগ কমবে। রেলগাড়িতে আপনার বিচারেও বাইরের জিনিসগুলির একই অবস্থা হবে।
কিন্তু সময় সাপেক্ষ ক্রিয়াগুলি হবে আরো অদ্ভূত।
এ ব্যাপারটা প্রায় আদর্শ প্রাঞ্জলতার সঙ্গে ব্যাখ্যা করেছিলেন এডিংটন। আমার উদাহরণের ভিত্তি তারই একটা উদাহরণ :
এমন একটা মহাকাশযান কল্পনা করুন যেটা প্রতি সেকেন্ডে পৃথিবী থেকে ১,৫৬,০০০ মাইল দূরে অপসৃত হচ্ছে। যদি আপনি মহাকাশযানের ভিতরকার মানুষদের পর্যবেক্ষণ করতে পারতেন তাহলে আপনার সিদ্ধান্ত হতো ওদের চলন অস্বাভাবিক মন্থর। মহাকাশযানের অন্যান্য ঘটনার গতিও একই রকম মন্থর মনে হতো। মনে হতো সেখানে সংগঠিত সমস্ত ঘটনাই সাধারণের চাইতে দ্বিগুণ সময় নিয়েছে। সিদ্ধান্ত (infer) কথাটা আমি বিশেষ বিবেচনা করেই ব্যবহার করেছি। আপনি কালের আরো অনেক বেশি মন্থরগতি লক্ষ্য করবেন। ব্যাপারটা বাখ্যা করা কিন্তু সহজ। কারণ আপনার কাছ থেকে মহাকাশযানের দূরত্ব দ্রুত বাড়ছে এবং আলোকবাহিত অনুভূতি (light impression) আপনার কাছে পৌঁছাতে বেশি বেশি সময় নিচ্ছে। আলোক প্রেরণের সময় বিচারের পর যা অবশিষ্ট থাকে সেটাই এর আগে স্বল্পতর মন্থরতারূপে উল্লেখ করা হয়েছে। কিন্তু এখানেও পারস্পরিক ক্রিয়ার (reciprocity) প্রশ্ন আসে। মহাকাশযানের যাত্রীদের দৃষ্টিভঙ্গিতে আপনি তাদের কাছ থেকে সেকেন্ডে ১,৫৬,০০০ মাইল দূরে অপসৃত হচ্ছেন এবং সব দিক হিসাব করার পর তারা দেখছে আপনিই মন্থর।
সময়ের এই প্রশ্নটা জটিল। তার কারণ যে সমস্ত ঘটনা একজনের বিচারে যুগপৎ অন্যের বিচারে সেগুলি কালিক ব্যবধান দিয়ে বিচ্ছিন্ন। সময় কি করে প্রভাবিত হয় সে তথ্য স্পষ্ট করার জন্য আমি আলোকের বেগের পাঁচ ভাগের তিন ভাগ বেগে সঠিক পূর্বদিকগামী রেলগাড়ি প্রসঙ্গে ফিরে যাব। উদাহরণ দেওয়ার স্বার্থে আমি অনুমান করব পৃথিবীটা বড় এবং চ্যাপ্টা–ছোট এবং গোলকাকৃতি নয়।
আমরা যদি পৃথিবীর একটি স্থির বিন্দুতে সংঘটিত একাধিক ঘটনা বিচার করি এবং নিজেদের প্রশ্ন করি ঘটনা শুরু করার কতক্ষণ পর যাত্রীরা সেগুলি বুঝতে পারবে তাহলে তার উত্তর হবে : এডিংটন উল্লিখিত মন্থরতা এক্ষেত্রে থাকবে। অর্থাৎ মাটিতে যাঁরা তাঁদের কাছে যে কাল একঘণ্টা মনে হবে, রেলগাড়ি থেকে যারা পর্যবেক্ষণ করছেন তাদের বিচারে সে কাল মনে হবে সোয়া একঘণ্টা এবং ব্যাপারটা হবে পারস্পরিক। পারস্পরিকভাবে ট্রেনের লোকের জীবনে যে কাল একঘণ্টা মনে হবে বাইরের লোক পর্যবেক্ষণ করলে তাদের বিচারে মনে হবে সে কাল সোয়া একঘণ্টা। প্রত্যেকেই অপরের জীবনের কালকে সে জীবন যারা যাপন করছে তাদের তুলনায় এক-চতুর্থাংশ বাড়িয়ে দেখে। কালের ক্ষেত্রের মতো দৈর্ঘ্যের ক্ষেত্রেও অনুপাত একই।
কিন্তু পৃথিবীর একই স্থানের বিভিন্ন ঘটনার ভিতরে তুলনা না করে বিরাট দূরত্ব দ্বারা বিচ্ছিন্ন ঘটনাবলী তুলনা করলে ফল হয় আরো অদ্ভুত। এবার রেললাইন বরাবর সমস্ত ঘটনা বিচার করা যাক। পৃথিবীতে যারা স্থিরাবস্থায় রয়েছেন তাঁদের দৃষ্টিভঙ্গি থেকে ঘটনাগুলি ঘটছে একটি বিশেষ মুহূর্তে ধরুন যে মুহূর্তে রেলগাড়িটা একটা বিশেষ সিগন্যাল অতিক্রম করছে। এই ঘটনাগুলির ভিতরে যেগুলির ঘটনাস্থল রেলগাড়ির গতির অভিমুখে কোনো বিন্দুতে যাত্রীদের মনে হবে ঘটনাগুলি আগেই ঘটে গিয়েছে। আবার যেগুলির ঘটনাস্থল রেলগাড়ির পিছনে সে ঘটনাগুলি আগেই ঘটে গিয়েছে। আবার যেগুলির ঘটনাস্থল। রেলগাড়ির পিছনে সে ঘটনাগুলিকে তখনো ভবিষ্যতের গর্ভে মনে হবে। যখন আমি বলছি মনে হবে সম্মুখের ঘটনাগুলি আগেই ঘটেছে তখন কিন্তু আমার বক্তব্য সম্পূর্ণ নির্ভুল নয়। কারণ ঘটনাগুলি তারা তখনো দেখেনি। ঘটনাগুলি যখন তারা দেখবে তখন আলোকের গতিবেগ হিসাব করে তাদের সিদ্ধান্ত হবে এই ঘটনাগুলি নিশ্চয়ই ঘটেছে আলোচ্য মুহূর্তের আগে। যে ঘটনা রেললাইন বরাবর সম্মুখ অভিমুখে ঘটে এবং স্থির পর্যবেক্ষকদের বিচারে বর্তমান মুহূর্তে ঘটে। কিংবা যখন তারা জানতে পারে তখন তাদের বিচারে বর্তমান মুহূর্ত (now) হয় এবং যদি রেললাইন বরাবর এতটা দূরত্বে ঘটে থাকে যে দূরত্ব অতিক্রম করতে আলোকের এক সেকেন্ড লাগে তাহলে যাত্রীরা ভাববে ঘটনাটি ঘটেছে এক সেকেন্ডের তিন-চতুর্থাংশ ভাগ আগে। ঘটনাটি যদি এমন দূরত্বে ঘটে আলোকের যে দূরত্ব অতিক্রম করতে পৃথিবীর লোকের বিচারে এক বছর লাগে তাহলে যাত্রীদের বিচারে (তারা যখন ঘটনাটি জানতে পারবে) ঘটনাটি ঘটেছে তারা পৃথিবীবাসীদের যে মুহূর্তে অতিক্রম করেছে তার নয় মাস আগে। এবং সাধারণভাবে, তাদের নিজেদের কাছ থেকে, যে পৃথিবীবাসীদের তারা যেই মুহূর্তে অতিক্রম করছে তাদের কাছে আলোকের পৌঁছাতে যে সময় লাগে রেললাইন বরাবর সম্মুখবর্তী স্থানে সংঘটিত ঘটনাবলীকে তারা তার তিন-চতুর্থাংশ পূর্ববর্তী কালাঙ্কা আরোপ করবে। পৃথিবীবাসীরা কিন্তু বিশ্বাস করবে ঘটনাটি ঘটছে এখুনি কিংবা তারা বরং বিশ্বাস করবে ঘটছে এখুনি অর্থাৎ ঘটনাস্থল থেকে আলোক যখন তাদের কাছে পৌঁছাচ্ছে তখন। রেলগাড়ির পশ্চাতে রেললাইনে সংঘটিত ঘটনাগুলিকে নির্ভুল একই পরিমাণে পরবর্তী কালাঙ্কা দেওয়া হবে (post date)।
সুতরাং পার্থিব পর্যবেক্ষকের কাছ থেকে যাত্রীদের কাছে উত্তরণের জন্য কালাঙ্কের দু’রকম সংশোধন আমাদের করতে হবে। প্রথমে আমাদের নিতে হবে পৃথিবীবাসীদের গণনার পাঁচ চতুর্থাংশ (five-fourths)। তারপর তা থেকে আমাদের বাদ দিতে হবে আলোচ্য ঘটনা থেকে আলোকের পৃথিবীবাসীদের কাছে আসতে যে কাল লাগে তার তিন চতুর্থাংশ।
দুরে মহাবিশ্বে সংঘটিত একটি ঘটনা বিচার করুন। পৃথিবীবাসীরা এবং যাত্রীরা যখন পরস্পরকে অতিক্রম করছে ঘটনাটা দৃষ্ট হচ্ছে ঠিক সেই সময়। ঘটনাটা কতদূরে ঘটেছিল সেটা যদি পৃথিবীবাসীদের জানা থাকে তাহলে তারা বিচার করতে পারে ব্যাপারটা যদি যাত্রীদের গতির অভিমুখে ঘটে থাকে তাহলে যাত্রীদের সিদ্ধান্ত হবে পৃথিবীবাসীরা যা ভেবেছে তার দ্বিগুণ আগে ঘটনাটা ঘটেছিল। কিন্তু যাত্রীরা যেদিক থেকে আসছে ঘটনাটা সেদিকে ঘটে থাকলে তারা বলবে পৃথিবীবাসীরা যা ভেবেছে ঘটনাটা ঘটেছে তার অর্ধেক সময় আগে। যাত্রীদের দ্রুতি ভিন্ন হলে এই অনুপাতগুলিও ভিন্ন হবে।
অনুমান করা যাক দু’টি তারকা হঠাৎ জ্বলে উঠেছে (মাঝে মাঝে এরকম ঘটে) এবং যাত্রীরা যখন পৃথিবীবাসীদের অতিক্রম করছিল তখন দু’পক্ষই সেটা দেখতে পেয়েছে। একটি হোক, রেলগাড়ি যেদিকে চলেছে সেদিকে এবং অন্যটি হোক, রেলগাড়ি যেদিক থেকে আসছে সেদিকে। অনুমান করা যাক পৃথিবীবাসীরা কোনো উপায়ে দুটি তারকার দূরত্ব নির্ধারণ করতে পেরেছে এবং তারা সিদ্ধান্ত করেছে যেদিকে যাত্রীরা চলেছে সেদিককার তারকা থেকে তাদের কাছে আলো পৌঁছাতে পঞ্চাশ বছর লাগে এবং অন্য তারকা থেকে তাদের কাছে আসতে আলোকের লাগে একশ বছর। তখন পৃথিবীবাসীদের যুক্তি হবে : যে বিস্ফোরণের ফলে সামনের তারকাটির জন্ম হয়েছে সেটা ঘটেছে পঞ্চাশ বছর আগে, আর যে বিস্ফোরণের ফলে নতুন তারকাটি জন্মেছে সেটা ঘটেছে একশ’ বছর আগে। যাত্রীরা কিন্তু এ অঙ্ক উল্টে দেবে : তাদের সিদ্ধান্ত হবে সম্মুখের বিস্ফোরণ হয়েছে। একশ’ বছর আগে আর পঞ্চাশ বছর আগে হয়েছে পিছনের বিস্ফোরণ। আমি ধরে নিচ্ছি উভয় পক্ষের যুক্তিই নির্ভুল এবং সে যুক্তির ভিত্তি নির্ভুল ভৌত উপাত্ত (data) আসলে উভয় পক্ষই নির্ভুল; অবশ্য যদি তারা মনে না করে যে অন্য পক্ষ নিশ্চয়ই ভুল করেছে। এটা মনে রাখতে হবে যে আলোর বেগ সম্পর্কে অনুমান (esti mate) উভয় পক্ষের একই ছিল তার কারণ বিস্ফোরণের পর সময় সম্পর্কে তাদের অনুমানের পরিবর্তন এবং দুটি তারকার দূরত্ব সম্পর্কে তাদের অনুমানের পরিবর্তন হবে একেবারে আনুপাতিক। আসলে সম্পূর্ণ তত্ত্বটার একটা প্রধান উদ্দেশ্য হল, পর্যবেক্ষকের নিজস্ব গতি নির্বিশেষে সমস্ত পর্যবেক্ষক সাপেক্ষই আলোকের বেগ অভিন্ন, এই তথ্য প্রতিষ্ঠা করা। বৈজ্ঞানিক পরীক্ষাদ্বারা প্রমাণিত এই তথ্যের সঙ্গে প্রাচীন তত্ত্বের সঙ্গতি ছিল না এবং চরম প্রয়োজন ছিল চমকপ্রদ একটা কিছু মেনে নেওয়ার। অপেক্ষবাদ ঘটনার সঙ্গে যতটা সঙ্গতিপূর্ণ ঠিক ততটাই চমকপ্রদ। আসলে কিছুদিন পর এ তত্ত্বকে মোটেই আর চমকপ্রদ মনে হয় না।
আমাদের আলোচ্য তত্ত্বের অত্যন্ত গুরুত্বপূর্ণ আর একটি অবয়ব রয়েছে। সেটা হল : যদিও ভিন্ন ভিন্ন পর্যবেক্ষক সাপেক্ষ দূরত্ব এবং কাল (time) পরিবর্তিত হয় তবুও আমরা সেগুলি থেকে অন্তর (interval) নামক একটি পরিমাণ (quantity) আহরণ করতে পারি। সে পরিমাণ প্রতিটি পর্যবেক্ষক সাপেক্ষ অভিন্ন। বিশিষ্ট অপেক্ষবাদে ‘অন্তর পাওয়া যায় নিম্নলিখিত উপায়ে: দুটি ঘটনার অন্তবর্তী দূরত্বের বর্গ (square) হিসাব করুন এবং দুটি ঘটনার অন্তবর্তী কালে আলোক যে দূরত্ব অতিক্রম করে তার বর্গ হিসাব করুন। দুটির ভিতরে বৃহত্তর থেকে ক্ষুদ্রতরটি বিয়োগ করুন। বিয়োগফল ঘটনাগুলির অন্তরের বর্গ বলে সংজ্ঞিত (defined)। অন্তর সমস্ত পর্যবেক্ষক সাপেক্ষ অভিন্ন এবং দুটি ঘটনার একটি ভৌত সম্পর্কের আসল প্রতিরূপ। স্থান এবং কাল কিন্তু সে রকম প্রতিরূপ নয়। চতুর্থ অধ্যায়ের শেষে অন্তরের একটি জ্যামিতিক গঠন আমরা দিয়েছি। ঐ গঠন উপরে লিখিত নিয়মের মতো একই ফল প্রদান করে। একটি ঘটনাস্থল থেকে অন্য ঘটনাস্থলে যেতে আলোকের যে কাল প্রয়োজন, দুটি ঘটনার অন্তবর্তী কাল যখন তার চাইতে দীর্ঘ, অন্তর তখন কালানুরূপ। বিপরীত ক্ষেত্রে অন্তর স্থানানুরূপ। যখন দুটি ঘটনার অন্তবর্তীকাল এবং আলোকের একস্থান থেকে অন্য স্থানে গমনকাল নির্ভুল অভিন্ন, অন্তর যখন শূন্য (zero) তখন ঘটনা দুটি একই আলোকরশ্মির বিভিন্ন অংশে অবস্থিত। অবশ্য ঐ পথে গমনশীল কোনো আলোকরশ্মি যদি না থাকে।
ব্যাপক অপেক্ষবাদে এসে আমাদের অন্তর সম্পর্কীয় ধারণার সাধারণীকরণ করতে হবে। বিশ্বের গঠনের যত গভীরে আমরা প্রবেশ করি এই কল্পনের গুরুত্ব ততই বৃদ্ধি পায়। আমাদের বলতে আকাঙখা হয় এটাই বাস্তব। দূরত্ব এবং ব্যাপ্তিকাল সে বাস্তবের বিভ্রান্ত প্রতিরূপ মাত্র (confused representation)। অপেক্ষাবাদ বিশ্বের মূলগত গঠন সম্পর্কে আমাদের ধারণা বদলে দিয়েছে। এই জন্যই এ তত্ত্ব দুরূহ, এ তত্ত্বের গুরুত্বও এই জন্য।
যে সমস্ত পাঠকের জ্যামিতি এবং বীজগণিতের সঙ্গে প্রাথমিক পরিচয়ও নেই তারা এই অধ্যায়ের অবশিষ্ট অংশ বাদ দিতে পারেন। যাঁদের শিক্ষা একদম অবহেলিত হয়নি তাঁদের জন্য সাধারণ সঙ্কেত (general formula) খানিকটা ব্যাখ্যা করব। এ পর্যন্ত সে সঙ্কেতের কয়েকটি বিশেষ উদাহরণ মাত্র আমি দিয়েছি। আলোচ্য সাধারণ সঙ্কেতের নাম লোরেঞ্জ রূপান্তর। এর বক্তব্য : একটি বস্তুপিণ্ড যখন অন্য একটি বস্তুপিণ্ড সাপেক্ষ নির্দিষ্ট প্রণালীতে চলমান তখন একটি বস্তুপিণ্ডের সঠিক দৈর্ঘ্য এবং কালের ভিত্তিতে কি করে অন্য বস্তুপিণ্ডের সঠিক দৈর্ঘ্য এবং কাল নির্ণয় করা যায়। বীজগণিতের সঙ্কেত দেওয়ার আগে আমি একটি জ্যামিতিক গঠন উপস্থিত করব। আগের মতোই আমি দু’জন পর্যবেক্ষক অনুমান করব, তাদের নাম দেব 0 এবং O’। এদের একজন পৃথিবীতে স্থিতিশীল এবং অন্যজন একটি ঋজুরেলপথে সমরূপ গতিতে চলমান। বিচার্যকালের শুরুতে দু’জন পর্যবেক্ষকেরই অবস্থান ছিল রেলপথের একটি বিন্দুতে; কিন্তু এখন তারা খানিকটা দূরত্বে বিচ্ছিন্ন। রেলপথের X বিন্দুতে একটি বাজ পড়েছে। O-এর বিচারে বাজ পড়ার মুহূর্তে রেলগাড়ির পর্যবেক্ষক ‘O’ বিন্দুতে পৌঁছেছে। সমস্যা হল : বিদ্যুতের চমক থেকে O’–এর দূরত্ব কত এবং O’-এর বিচারে যাত্রা শুরু হওয়ার (যখন O এবং O’ একসঙ্গে ছিল) কতক্ষণ পর ঘটনাটা ঘটেছিল। O-এর অনুমান (estimate) আমাদের জানবার কথা এবং আমরা O’–এর অনুমান গণনা করতে চাই।
O-এর বিচারে যাত্রারম্ভের পর যে কাল অতিক্রান্ত হয়েছে সেইকালে রেলপথ বরাবর আলোক যে দূরত্ব অতিক্রম করত OC হোক সেই দূরত্ব। 0 কে কেন্দ্র করে OC কে ব্যাসার্ধ নিয়ে একটি বৃত্ত অঙ্কন করুন।
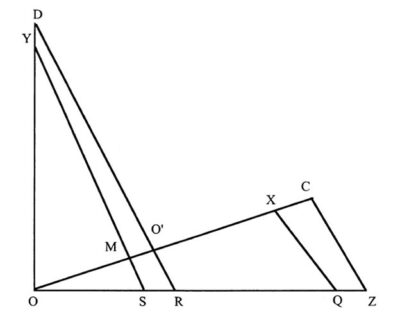
O’-এর ভিতর দিয়ে রেলপথের উপর একটি লম্ব আঁকুন। লম্বটি D বিন্দুতে বৃত্তের সঙ্গে মিলিত হোক। OD-এর উপরে এমন একটি বিন্দু Y নিন যাতে OY এবং OX সমান হয় (রেলপথের X বিন্দুতে বজ্রাঘাত হয়েছে)। রেলপথের উপর YM লম্ব আঁকুন এবং OD এর উপর OS লম্ব আঁকুন। YM এবং OS, S বিন্দুতে মিলিত হোক। DO’ এবং OS কে বাড়িয়ে R বিন্দুতে মিলিত করা হোক। X এবং C এর ভিতর দিয়ে রেলপথের উপর লম্ব আঁকুন। OS কে বাড়িয়ে দিন। লম্ব দুইটি বাড়িয়ে দেওয়া OS এর সঙ্গে Q এবং Z বিন্দুতে মিলিত হোক। তাহলে O’ এর বিচারে O’ থেকে বজ্রপাতের দূরত্ব (O এর মাপন অনুসারে) RQ। প্রাচীন ধারণা অনুসারে দূরত্ব হওয়া উচিত ছিল OX। যেমন 0 ভাবছে যাত্রারম্ভ থেকে বজ্রপাত পর্যন্তকালে আলোক OC দূরত্ব অতিক্রম করত। O’ ভাবছে এই অতিক্রান্ত সময় এবং আলোকের SZ. দূরত্ব (0 এর মাপন অনুসারে) অতিক্রম করার সময় একই। ০ এর মাপনানুযায়ী অন্তর পাওয়া গিয়েছে OC এর উপর অঙ্কিত সমচতুর্ভুজ (square) থেকে OX এর উপর অঙ্কিত সমচতুর্ভুজ বিয়োগ করে। O’ এর মাপনানুযায়ী অন্তর পাওয়া গিয়েছে SZ এর উপর অঙ্কিত সমচতুর্ভুজ থেকে RQ এর উপর অঙ্কিত সমচতুভুজ বিয়োগ করে। সামান্য প্রাথমিক জ্যামিতি থেকে বোঝা যায় এ দুটি সমান।
উপরের গঠনক্রিয়ার অঙ্গীভূত (embodied) বীজগণিত সঙ্কেত নিম্নরূপ : ০ এর দৃষ্টিভঙ্গি থেকে রেলপথ বরাবর X দূরত্বে এবং যাত্রা শুরু করার পর (যখন o’ ছিল ০-তে) T কাল বাদে একটি ঘটনা ঘটুক। O’ এর দৃষ্টিভঙ্গিতে রেলপথ বরাবর X’ দূরত্বে, যাত্রারম্ভের পর T’ কাল বাদে একই ঘটনা ঘটুক।
আলোকের বেগ হোক C এবং O সাপেক্ষে O’ এর বেগ হোক v। স্থাপন করুন–
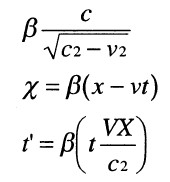
তাহলে, এটাই লোরেঞ্জ রূপান্তর। এ থেকেই এ অধ্যায়ের সব কিছু উপপাদন সম্ভব।
