০৫. স্থান কাল

৫. স্থান কাল

অপেক্ষবাদ সম্পর্কে যারা কখনো শুনেছেন তাঁদের সবাই স্থান-কাল’ কথাটা জানেন এবং এও জানেন যে এই কথাটাই শুদ্ধ এবং আগেকার দিনে আমাদের বলতে হতো স্থান এবং কাল’ । কিন্তু যারা গণিতবিদ নন তাদের ভিতরে খুব কম লোকেরই বাগ্বিধির এই পরিবর্তন সম্পর্কে স্পষ্ট ধারণা আছে। বিশিষ্ট অপেক্ষবাদ নিয়ে আর অগ্রসর হওয়ার আগে এই নতুন শব্দসমষ্টি স্থান-কালের সঙ্গে কি জড়িত রয়েছে সেটাই আমি পাঠকদের কাছে উপস্থিত করার চেষ্টা করব। কারণ, আইনস্টাইন যে সমস্ত নতুনত্ব উপস্থাপন করেছেন সেগুলির ভিতরে দর্শন (philo sophical) এবং কল্পনের (imaginatics) দিক থেকে সবচাইতে গুরুত্বপূর্ণ এটাই।

অনুমান করা যাক একটি ঘটনা যেমন বিমানে একটি বিস্ফোরণ– কোথায় কখন ঘটেছে– আপনি সেটা বলতে চান, তাহলে আপনাকে উল্লেখ করতে হবে চারটি রাশি–অক্ষাংশ (Latitude), দ্রাঘিমা (Longitude), জমি থেকে উচ্চতা এবং কাল। চিরায়ত দৃষ্টিভঙ্গি অনুসারে এগুলির ভিতরে প্রথম তিনটি প্রকাশ করে স্থানে অবস্থান এবং চতুর্থটি প্রকাশ করে কালে অবস্থান। যে তিনটি রাশি (quan tity) স্থানে অবস্থান প্রকাশ করে সেগুলিকে নানাভাবে আরোপ করা সম্ভব। উদাহরণ : আপনি বিষুবরেখার তল (plane) গ্রহণ করতে পারেন, গ্রিনউইচের মধ্যরেখার (meridian) তল গ্রহণ করতে পারেন, গ্রহণ করতে পারেন নবতিতম মধ্যরেখার তল এবং এর প্রতিটি তল থেকে বিমানটি কতদূরে ছিল সে কথা বলতে পারেন। দেকার্তের (Descartes) নাম অনুসারে যাকে কার্তেজীয় স্থানাঙ্ক (Cartesian Co-ordinate) বলা হয়, এই তিনটি দূরত্ব হল তাই। পরস্পর সমকোণ সম্পর্কযুক্ত অন্য যে কোনো তিনটি তল (plane) আপনি নিতে পারেন। তখনো আপনি কার্তেজীয় স্থানাঙ্ক পাবেন। কিংবা আপনি নিতে পারেন লণ্ডন থেকে উল্লম্বভাবে বিমানের নিচের বিন্দু পর্যন্ত দূরত্ব, এই দূরত্বের অভিমুখ (উত্তর পূর্ব, পশ্চিম, দক্ষিণ-পশ্চিম কিংবা যাই হোক) এবং মাটি থেকে বিমানের উচ্চতা। স্থানে অবস্থান নির্দিষ্ট করার এরকম পদ্ধতি সংখ্যা অসীম এবং প্রত্যেকটি পদ্ধতি একই রকম বিধিসঙ্গত (legitimate)। এগুলির ভিতর থেকে একটিকে নির্বাচনের কারণ শুধুমাত্র সুবিধা।

লোকে যখন বলত স্থানের তিনটি মাত্রা তখন তাদের কথার অর্থ ছিল ঠিক এই : স্থানে একটি বিন্দুর অবস্থান নির্দেশ করতে তিনটি রাশি প্রয়োজন। কিন্তু এই রাশিগুলি আরোপ করার পদ্ধতি ছিল সম্পূর্ণ যাদৃচ্ছিক।

কাল বিষয়ে ভাবা হতো : ব্যাপারটা সম্পূর্ণ পৃথক। কাল গণনার একমাত্র যাদৃচ্ছিক উপাদান ছিল কালের একক এবং কাল গণনার আরম্ভ বিন্দু। গ্রিনউইচের কাল, প্যারিসের কাল কিংবা নিউ ইয়র্কের কাল অনুসারে গণনা করা যেত–এতে পার্থক্য হতো প্রস্থান বিন্দুর (point of departure)। সেকেন্ডে, ঘণ্টায়, দিনে কিংবা বছরে গণনা করা যেত– সে ক্ষেত্রে পার্থক্য হতো এককের। এ ব্যাপারগুলো কিন্তু ছিল স্বতঃপ্রতীয়মান এবং তুচ্ছ। অবস্থান নির্দিষ্ট করার পদ্ধতির ব্যাপারে স্থানের অনুরূপ কোনো নির্বাচনের স্বাধীনতা ছিল না। তাছাড়া বিশেষ করে ভাবা হতো স্থানে অবস্থান নির্দিষ্ট করার পদ্ধতি এবং কালে অবস্থান নির্দিষ্ট করার পদ্ধতি–এ দুটিকে পরস্পর সাপেক্ষ সম্পূর্ণ স্বতন্ত্র করা সম্ভব। এই সমস্ত কারণে লোকে ভাবত স্থান এবং কাল সম্পূর্ণ পৃথক।

এ বিষয়ে পরিবর্তন এনেছে অপেক্ষবাদ। কালে অবস্থান নির্দিষ্ট করার এখন একাধিক বিভিন্ন পদ্ধতি রয়েছে। পদ্ধতিগুলির ভিতরে পার্থক্য শুধু একক এবং আরম্ভ বিন্দুর নয়। আসলে আগে আমরা দেখেছি এরকম গণনায় যদি একটি ঘটনা অন্য একটি ঘটনার সঙ্গে যুগপৎ হয় তাহলে অন্য গণনায় সেটা অগ্রবর্তী হবে এবং তৃতীয় একটি গণনায় সেটা হবে পশ্চাদ্বর্তী। তাছাড়া স্থান এবং কাল গণনা এখন আর পরস্পর থেকে স্বতন্ত্র নয়। আপনি যদি স্থানে অবস্থান গণনা করার পদ্ধতি পরিবর্তন করেন তাহলে হয়তো আপনি দুটি ঘটনার কাল অন্তরও পরিবর্তন করবেন। আপনি যদি কাল গণনার পদ্ধতির পরিবর্তন করেন তাহলে হয়তো আপনি স্থানে দুটি ঘটনার দূরত্বেরও পরিবর্তন করতে পারেন। সুতরাং স্থান এবং কাল এখন আর স্বতন্ত্র নয়। স্থানের তিন মাত্রায় যে স্বাতন্ত্র তার চাইতে বেশি স্বাতন্ত্র কালের নেই। একটি ঘটনার অবস্থান নির্ণয় করতে এখনো আমাদের চারটি রাশিই লাগে কিন্তু আগের মতো এখন আমরা একটিকে অন্য তিনটে থেকে স্বতন্ত্র ভাবতে পারি না।

স্থান এবং কালে কোনো পার্থক্য আর নেই এ বিবৃতি কিন্তু সম্পূর্ণ সত্য নয়। আমরা আগে দেখেছি কালানুরূপ অন্তর এবং স্থানানুরূপ অন্তরের অস্তিত্ব রয়েছে। আগে যেরকম অনুমান করা হতো এ পার্থক্যটা তার চাইতে অন্যরকম। মহাবিশ্বের সর্ব অংশে প্রযোজ্য কোনো দ্ব্যর্থবোধহীন (Without ambiguity) সার্বিক কালের অস্তিত্ব নেই। শুধুমাত্র রয়েছে মহাবিশ্বের নানা বস্তুপিণ্ড সাপেক্ষ নানা ‘বিশিষ্ট’ (proper) কাল। যে দুটি বস্তুপিণ্ড দ্রুত চলমান নয়– তাদের বিশিষ্ট কালের ভিতরে আসন্ন (approximate) ঐক্য রয়েছে। কিন্তু যে বস্তুপিণ্ডগুলি পরস্পর সাপেক্ষ সম্পূর্ণ স্থিতিশীল সেগুলির ক্ষেত্রে ছাড়া এ ঐক্য কখনোই সম্পূর্ণ হতে পারে না।

ঘটনাবলীর এই পরিপ্রেক্ষিতে যে বিশ্বচিত্র প্রয়োজন তার রূপ এইরকম : ধরুন আমাতে একটি ঘটনা E ঘটেছে এবং যুগপৎ আমার কাছ থেকে সবদিকে একটি আলোর ঝলক বহির্গত হয়েছে। আলোর ঝলক একটি বস্তুপিণ্ডে পৌঁছানোর পর সে বস্তুপিণ্ডে যাই ঘটুক না কেন সেগুলি ঘটেছে নিশ্চিতভাবে ঘটনা E এর পর। কাল গণনা যে তন্ত্র হিসাবে হোক না কেন (any system of reckoning), এ তথ্য সত্য। হবে। আমার ভিতরে ঘটনা E ঘটবার আগে আমি যদি যে কোনো জায়গায় ঘটিত কোনো ঘটনা দেখে থাকি তাহলে সে ঘটনা নিশ্চিতভাবে E এর আগে ঘটেছে কাল গণনার যে কোনো তন্ত্র অনুসারে এ তথ্য সত্য। কিন্তু অন্তবর্তীকালে সংঘটিত কোনো ঘটনা নিশ্চিতভাবে E ঘটনার আগে কিংবা পরে নয়। ব্যাপারটাকে আরো নির্দিষ্ট নিশ্চিত করার জন্য উদাহরণ : অনুমান করা যাক আমি সিরিয়াসের (Serius) এক। ব্যক্তিকে পর্যবেক্ষণ করতে পারি এবং সেই সিরিয়াসবাসীও আমাকে পর্যবেক্ষণ করতে পারে। আমাতে ঘটনা E ঘটনার আগে সিরিয়াসবাসী করেছে এরকম যা আমি দেখতে পাই সেগুলি নিশ্চিতভাবে E এর পূর্ববর্তী। ঘটনা E দেখবার আগে সিরিয়াসবাসীর করা যা কিছু আমি E ঘটবার পর দেখতে পাই সেগুলি নিশ্চিতভাবে E এর আগে কিংবা পরে নয়। আলোকের সিরিয়াস থেকে পৃথিবীতে পৌঁছাতে সাড়ে আট বছর লাগে সুতরাং এ থেকে সিরিয়াসে আমরা সতের বছর সময় পাই যে সময়কে আমরা বলতে পারি E এর সমসাময়িক (contemporary)-কারণ এ ঘটনাগুলি নিশ্চিতভাবে E-এর আগে কিংবা পরে নয়।

ডা. এ. এ. রব (Dr. A. A Robb) তার স্থান এবং কাল বিষয়ক তত্ত্ব’ (theory of time and space) পুস্তকে একটি দৃষ্টিভঙ্গির কথা বলেছেন সে দৃষ্টিভঙ্গি দর্শন শাস্ত্রের দিক থেকে মূলগত হতে পারে, নাও হতে পারে। সেই যা হোক, যে ব্যাপারটার বিবরণ দিতে আমরা চেষ্টা করছি সেটা বুঝতে এ দৃষ্টিভঙ্গি আমাদের সাহায্য করবে। তার মতে একটি ঘটনাকে অন্য একটি ঘটনার নিশ্চিত পূর্বগামী বলা যায় তখনই যখন সে ঘটনা অন্য ঘটনাটিকে কোনোভাবে প্রভাবিত করে। একটি কেন্দ্র থেকে প্রভাব বিস্তৃত হয় নানা হারে। লন্ডন থেকে উদ্ভূত সংবাদপত্রের প্রভাব ঘণ্টায় কুড়ি মাইল হারে বিস্তার লাভ করে–দূরত্ব দীর্ঘতর হলে এর চাইতে একটু বেশি হারেও করে।

সংবাদপত্রে প্রবন্ধ পাঠের ফলে একটি লোক যা কিছু করে সেগুলি স্পষ্টতই সংবাদপত্র মুদ্রণের পরবর্তী। শব্দ অনেক বেশি দ্রুতগামী। রাজপথ বরাবর লাউডস্পিকারের সার বসিয়ে কাগজের খবর একটা থেকে পরেরটায় চেঁচিয়ে বলা সম্ভব। কিন্তু টেলিগ্রাফ যায় আরো তাড়াতাড়ি আর রেডিও সঙ্কেত চলে আলোর বেগে সুতরাং এর চাইতে দ্রুত কিছু আশা করা যায় না। কোনো ব্যক্তি বেতার বার্তা পাওয়ার ফলে যে কাজ করে সে কাজ করা হয় বার্তা প্রেরণের পর; এক্ষেত্রে পরবর্তী শব্দের অর্থ কাল মাপনের রীতি নিরপেক্ষ। কিন্তু বার্তা যখন চলার পথে তখন যা করা হয় সেগুলি বার্তা প্রেরণের দ্বারা প্রভাবিত হতে পারে না এবং বার্তা প্রেরণের সামান্য কাল পরে ছাড়া বার্তা প্রেরককে প্রভাবিত করতে পারে না। সেই সময় অতিবাহিত হওয়ার আগে যা ঘটে সে ঘটনা দূরবর্তী বস্তুপিণ্ডকে প্রভাবিত করতে পারে না। দৃষ্টান্ত : অনুমান করা যাক সূর্যে একটি লক্ষণীয় ঘটনা ঘটেছে। ষোল মিনিট পর্যন্ত পৃথিবীর কোনো ঘটনা সূর্যের সেই ঘটনাকে প্রভাবিত করতে পারে না কিংবা সে ঘটনার দ্বারা প্রভাবিত হতে পারে না। ফলে পৃথিবীর ষোল মিনিট কালকে সূর্যের ঘটনার পূর্ববর্তী কিংবা পরবর্তী না ভাববার বাস্তব যুক্তি রয়েছে।

বিশিষ্ট অপেক্ষবাদের স্ববিরোধগুলিকে (paradox) স্ববিরোধী মনে হয় শুধুমাত্র আমরা ঐ দৃষ্টিভঙ্গির সঙ্গে পরিচিত নই বলে : এবং যে সমস্ত তথ্যকে সত্য বলে মেনে নেওয়ার কোনো অধিকার আমাদের নেই, সেই সমস্ত তথ্যকে সত্য বলে গ্রহণ করার অভ্যাসের দরুন। দৈর্ঘ্য মাপন ব্যাপারে এ তথ্য বিশেষভাবে সত্য। দৈনন্দিন জীবনে আমাদের দৈর্ঘ্য মাপনের পদ্ধতি ফুটরুল (foot rule) কিংবা অন্য কোনো মানদণ্ড প্রয়োগ করা। প্রয়োগের মুহূর্তে ফুটরুলটি যে জিনিসটিকে মাপা হচ্ছে সেটি সাপেক্ষ স্থিতিশীল। সুতরাং মাপনের সাহায্যে যে দৈর্ঘ্য পাওয়া যায় সেটাই ‘সঠিক’ (proper) দৈর্ঘ্য। অর্থাৎ সে দৈর্ঘ্য স্থির করেছেন এমন একজন পর্যবেক্ষক যিনি ঐ বস্তৃপিণ্ডের গতির অংশীদার। সাধারণ জীবনে আমাদের কখনোই অবিরাম চলমান বস্তুপিণ্ড মাপনের সমস্যা সমাধান করতে হয় না। পৃথিবীর বেগের তুলনায় পৃথিবীতে অবস্থিত দৃশ্যমান বস্তুপিণ্ডগুলির বেগ এত কম যে আমাদের যদি সে সমস্যার সমাধান করতে হতো তাহলেও অপেক্ষবাদ যে সমস্ত অসঙ্গতি নিয়ে বিচার করেছে সেগুলি প্রকাশ পেত না। কিন্তু জ্যোতির্বিজ্ঞানে কিংবা আণবিক গঠন অনুসন্ধানে আমরা এমন কতগুলি সমস্যায় পড়ি যেগুলির সমাধান এভাবে সম্ভব নয়। আমরা যোশুয়া (Joshua) নই সুতরাং মাপবার সময় সূর্যকে আমরা স্থিতিশীল করতে পারি না। সূর্যের আয়তন পরিমাপ করতে হলে করতে হবে সূর্য যখন পৃথিবী সাপেক্ষ চলমান তখনই। ইলেকট্রন সাপেক্ষও ব্যাপারটা একই। ইলেকট্রন মাপতে হবে দ্রুত চলমান অবস্থায়। কারণ ইলেকট্রন মুহূর্তের জন্যও স্থির থাকে না। এই রকম সমস্যা নিয়ে অপেক্ষবাদের চিন্তন। ফুটরুল দিয়ে যখন মাপা সম্ভব তখন মাপনফল সবসময়ই এক হয়। কারণ এ পদ্ধতিতে আমরা পাই বস্তুপিণ্ডের ‘সঠিক’ (proper নিজস্ব) দৈর্ঘ্য। এ পদ্ধতি যখন সম্ভব নয় বিশেষ করে যে বস্তুপিণ্ডকে মাপতে হবে সেটা যখন পর্যবেক্ষক সাপেক্ষ দ্রুত চলমান তখন অদ্ভুত সব ব্যাপার ঘটে। ব্যাপারটা বুঝতে হলে আগের অধ্যায়ের শেষের চিত্রটির মতো একটা চিত্র আমাদের সাহায্য করতে পারে।

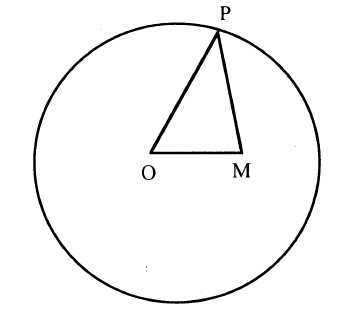
অনুমান করা যাক যে বস্তুপিণ্ডের দৈর্ঘ্য আমরা মাপতে চাই সেটা আমরা সাপেক্ষ চলমান এবং সেটি এক সেকেন্ডে OM দৈর্ঘ্য অতিক্রম করে। 0 কে কেন্দ্র করে একটি বৃত্ত আঁকা যাক। আলোক এক সেকেন্ডে যে দূরত্ব অতিক্রম করে সেটা হবে বৃত্তের ব্যাসার্ধ। M থেকে OM এর উপর MP লম্ব আঁকুন। লম্বটি বৃত্তের সঙ্গে মিলিত হবে P বিন্দুতে। তাহলে OP হবে আলোক এক সেকেন্ডে যে দূরত্ব অতিক্রম করে তার সমান। OP এর সঙ্গে OM–র অনুপাত তাহলে আলোকের বেগের সঙ্গে বস্তুপিণ্ডের বেগের অনুপাত। গতির ফলে আপাতদৃষ্ট দৈর্ঘ্যের যে পরিবর্তন হয় সেটা হল OP এর সঙ্গে MP–র অনুপাত। অর্থাৎ একজন পর্যবেক্ষকের বিচারে একটি চলমান বস্তুপিণ্ডের গতিরেখার দুটি বিন্দুর পারস্পরিক দূরত্বের প্রতিরূপ যদি MP হয় তাহলে ঐ বস্তুপিণ্ডের সঙ্গে চলমান একটি ব্যক্তির বিচারে ঐ দূরত্বে প্রতিরূপ (একই মাপক্রমে scale) হবে OP। চলমান বস্তুপিণ্ডের উপর গতিরেখার সমকোণীয় দূরত্ব গতিদ্বারা প্রভাবিত হয় না। পুরো ব্যাপারটাই পারস্পরিক (reciprocal)। অর্থাৎ বস্তুপিণ্ডটির সঙ্গে চলমান একজন পর্যবেক্ষক যদি আগের পর্যবেক্ষকের বস্তুপিণ্ডের উপরের দৈর্ঘ্য মাপেন তাহলে তার পরিবর্তন হবে একই অনুপাতে। দুটি বস্তুপিণ্ড যখন পরস্পর সাপেক্ষ চলমান তখন একটির উপরের দৈর্ঘ্য নিজেদের তুলনায় অপরের কাছে হস্বতর মনে হয়। এরই নাম লোরেঞ্জ সঙ্কোচন (Loreniz contraction)। মিচেলসন-মর্লি পরীক্ষাফল ব্যাখ্যা করার জন্য এ তথ্য প্রথম আবিষ্কৃত হয়। যুগপত্তা সম্পর্কে দু’জন পর্যবেক্ষকের বিচার এক হয় না। এই তথ্য থেকে লোরেঞ্চ সঙ্কোচন তত্ত্বের আবির্ভাব স্বাভাবিক।

যুগপত্তা আসছে এইভাবে : যখন আমরা একটি বস্তুপিণ্ডের দুটি বিন্দুর একটিতে ফুটরুলের একপ্রান্ত এবং অন্যটিতে ফুটবলের অন্যপ্রান্ত যুগপৎ’ প্রয়োগ করতে পারি তখন আমরা বলি বিন্দু দুটির দূরত্ব এক ফুট । কিন্তু দুটি ব্যক্তির যদি যুগপত্তা বিষয়ে মতানৈক্য থাকে এবং বস্তুপিণ্ডটি যদি চলমান হয় তাহলে তাদের দুজনের মাপনফল ভিন্ন ভিন্ন হবে এ তথ্য স্বতঃপ্রতীয়মান। সুতরাং দূরত্ব বিষয়ক সঙ্কটের মূলে রয়েছে কাল বিষয়ক সঙ্কট।

এই সমস্ত বিষয়ের মূলে রয়েছে (essential thing) OP-এর সঙ্গে MP–এর অনুপাত। আলোচ্য বস্তুপিণ্ড যখন পর্যবেক্ষক সাপেক্ষ চলমান তখন কাল, দৈর্ঘ্য এবং ভর এই অনুপাতে পরিবর্তিত হয়। দেখা যাবে OM যদি OP–এর তুলনায় খুব ছোট হয় অর্থাৎ বস্তুপিণ্ডের গতি আলোকের তুলনায় অত্যন্ত অল্প হলে MP এবং OP হবে প্রায় সমান সুতরাং গতির ফলে পরিবর্তনের পরিমাণ হবে অত্যন্ত অল্প। কিন্তু OM যদি OP-এর সমান হয় অর্থাৎ বস্তুপিণ্ডটির গতি যদি প্রায় আলোকের সমান হয় তাহলে OP-এর তুলনায় MP হয় অত্যন্ত ছোট এবং ক্রিয়াফল (effect) হয় অত্যন্ত বেশি। দ্রুতগামী বস্তুকণাগুলির ভরের আপাতদৃষ্ট বৃদ্ধি আগেই লক্ষ্য করা গিয়েছিল এবং বিশিষ্ট অপেক্ষবাদ আবিষ্কারের আগেই সঠিক সঙ্কেতও (formula) আবিষ্কৃত হয়েছিল। লোরেঞ্জ রূপান্তর (Lorentz transformation) নামক সঙ্কেত লোরেঞ্জ আবিষ্কার করেছিলেন। আসলে বিশিষ্ট অপেক্ষবাদের গাণিতিক সারাংশের (mathematical essence) সবটাই এ সঙ্কেতের অঙ্গীভূত। কিন্তু আইনস্টাইনই দেখিয়েছিলেন পুরো ব্যাপারটাই আশানুরূপ; বিস্ময়কর পরীক্ষাফল ব্যাখ্যা করার জন্য এক গুচ্ছ অস্থায়ী কৌশল মাত্র নয়। বৈজ্ঞানিক পরীক্ষালব্ধ ফলই ছিল সম্পূর্ণ তত্ত্বটির প্রাথমিক প্রেরণা; একথা কিন্তু ভুললে চলবে না। ভুললে চলবে না, অপেক্ষবাদের সঙ্গে জড়িত বিরাট যৌক্তি পুনর্গঠনের দায় গ্রহণ করার কারণ ছিল এই পরীক্ষাফল ।

এবার আমরা স্থান এবং কালের পরিবর্তে স্থান-কাল’ প্রতিস্থাপন করার প্রয়োজনগুলি পুনরাবৃত্তি করতে পারি, স্থান এবং কালের প্রাচীন বিচ্ছিন্নতা প্রতিষ্ঠিত ছিল এই বিশ্বাসের উপর; দূরস্থিত দুটি ঘটনা একই কালে ঘটেছে। এই কথার ভিতর দ্ব্যর্থবোধক কিছু নেই। সেই জন্য চিন্তা করা হতো যে কোনো একটি বিশেষ মুহূর্তে ব্রহ্মাণ্ডের সংস্থান বিবরণ (topography of the Universe) শুদ্ধ স্থানিক বাগ্বিধিতে (purely spatial terms) প্রকাশ করা সম্ভব। কিন্তু এখন যুগপত্তার অর্থ দাঁড়িয়েছে একজন বিশেষ পর্যবেক্ষক সাপেক্ষ যুগপত্তা, সুতরাং এ পদ্ধতি এখন অচল। একজন পর্যবেক্ষক সাপেক্ষ যেটা এক বিশেষ মুহূর্তে বিশ্বের অবস্থার বিবরণ আর একজন পর্যবেক্ষক সাপেক্ষ যেটা এক বিশেষ মুহূর্তে বিশ্বের অবস্থার বিবরণ আর একজন পর্যবেক্ষক সাপেক্ষ সেটা নানা ভিন্ন ভিন্ন কালের ঘটনার মালিকামাত্র। সে ঘটনাগুলির পারস্পরিক সম্পর্ক শুধু স্থানিক নয় কালিকও বটে। সেই জন্যই আমাদের বিচার ‘ঘটনা’ (events) নিয়ে, বস্তুপিণ্ড (body) নিয়ে নয়। আগেকার তত্ত্বে একই মুহূর্তে একাধিক বস্তুপিণ্ড সম্পর্কে বিচার সম্ভব ছিল। প্রতিটি বস্তুপিণ্ড সাপেক্ষ কাল ছিল অভিন্ন সুতরাং কালকে অগ্রাহ্য করা যেত। কিন্তু ভৌত ঘটনাগুলি সম্পর্কে বস্তুনিষ্ঠ তথ্য সংগ্রহ করতে হলে এখন আর আমরা কালকে অগ্রাহ্য করতে পারি না। একটি বস্তুপিণ্ড বিচারের কালাঙ্ক আমাদের উল্লেখ করতে হবে, এইভাবে আমরা উপনীত হব ঘটনায় অর্থাৎ একটি বিশেষ কালে ঘটমান একটা কিছুতে। একজন পর্যবেক্ষকের গণনাপদ্ধতি অনুসারে একটি ঘটনার স্থান এবং কাল জানলে আমরা অন্য পর্যবেক্ষক সাপেক্ষ সে ঘটনার স্থান এবং কাল গণনা করতে পারি। আগের পর্যবেক্ষকের ‘সমকালে’ (same time) পরের পর্যবেক্ষকের স্থান কোথায়? এ প্রশ্ন আর করা সম্ভব নয়। সুতরাং আমাদের স্থান এবং কাল দুটোই জানতে হবে, বিভিন্ন পর্যবেক্ষক পরস্পর সাপেক্ষ স্থিতিশীল না হলে তাদের সবার একই’ কালের কোনো অস্তিত্ব নেই। একটি অবস্থান নির্দিষ্ট করতে আমাদের চারটি মাপন প্রয়োজন। এই চারটি মাপন স্থান কালে একটি ঘটনার অবস্থান নির্দিষ্ট করে শুধুমাত্র স্থানে বস্তুপিণ্ডের অবস্থান নির্দিষ্ট করে না। একটি অবস্থান নির্দিষ্ট করতে তিনটি মাপন যথেষ্ট নয়। স্থান এবং কালের স্থলে স্থান-কাল’ প্রতিস্থাপনের অর্থের সারাংশ এটাই।