অধ্যায়-৫ – মহাবিশ্ব মুক্ত না কি বদ্ধ?

অধ্যায়-৫ – মহাবিশ্ব মুক্ত না কি বদ্ধ?

মহাবিশ্বের প্রসারণ কী চিরকালই চলবে কিংবা ভবিষ্যতে কিছুকাল পর এর প্রসারণ থেমে গিয়ে কী সংকোচন শুরু হবে? এই প্রশ্নটি সৃষ্টিতত্ত্বের সবচেয়ে গুরুত্বপূর্ণ, অমীমাংসিত জটিল প্রশ্নগুলোর মধ্যে প্রধান একটি। মহাবিশ্বের স্কেল ফ্যাক্টর ‘R’ কে বিবেচনায় এনে কিছু প্রশ্ন তৈরি করা যায় – ভবিষ্যতের সকল সময়ের জন্য R কী সময়ের সঙ্গে সঙ্গে বৃদ্ধিপ্রাপ্ত হবে না কি চূড়ান্ত অবস্থায় পৌঁছার পর ছোটো হতে থাকবে এবং অবশেষে শূন্যে পরিণত হবে? এই দুই সম্ভাবনাই ৫.১ নম্বর লেখচিত্রে দেখানো হয়েছে। মুক্ত মহাবিশ্ব চিরকালই সম্প্রসারিত হবে অর্থাৎ সাধারণ আন্তঃছায়াপথীয় (ইন্টারগ্যালাটিক) দূরত্বসমূহ অনন্তকাল ধরে বাড়তে থাকবে। অন্যদিকে মহাবিশ্ব বদ্ধ হলে সাধারণ গ্যালাক্সিসমূহের মধ্যবর্তী দূরত্বসমূহ একটি চূড়ান্ত মানে পৌঁছার পর এদের এই মধ্যবর্তী দূরত্বসমূহ কমতে শুরু করবে এবং সসীম সময়ে শূন্যতে পৌঁছবে। মহাবিশ্বের সাধারণ মডেলগুলোর প্রত্যেকটি যদি স্বয়ং নিজেকে নিজের গণ্ডিতে বেঁধে রাখে তাহলে মুক্ত মহাবিশ্ব তার ব্যাপ্তির দিক থেকে অসীম হবে আর বদ্ধ মহাবিশ্ব হবে সসীম। রাশিয়ার গণিতবিদ আলেকজান্ডার আলেকজান্দ্রোভিচ ফ্রিদম্যান (১৮৮৮-১৯২৫) মহাবিশ্বের এই সাধারণ মডেল দুটি প্রতিষ্ঠা করেছিলেন। তাই তাঁর নামানুসারে মডেলদ্বয়কে ফ্রিদম্যান মডেল বলা হয়। তিনি বিজ্ঞানী আইনস্টাইনের সমীকরণগুলোর রহস্যোদ্ঘাটন হিসেবে এই দুটি মডেল তৈরি করেছিলেন।

ফ্রিদম্যান মডেলগুলোর ক্ষেত্রে মুক্ত মহাবিশ্বের স্পেসের জ্যামিতি বদ্ধ মহাবিশ্বের স্পেসের জ্যামিতি থেকে ভিন্ন হবে। এই যুক্তিটি নিম্নরূপে বর্ণনা করা হল : সাধারণ স্থান অর্থাৎ প্রচলিত স্থান যাতে আমরা অভ্যস্থ, সে স্থানের ক্ষেত্রে (এই স্পেসকে ইউক্লেডের স্পেস বলা হয় কারণ এতে ইউক্লেডের জ্যামিতি চরিতার্থ) ক্ষেত্রে যদি একটি r ব্যাসার্ধের পরিমণ্ডল ধরে নেই এর পৃষ্ঠতলের ক্ষেত্রফল হয় 4πr^2 এবং আয়তন দাঁড়ায় (4/3)πr^2। একটি বদ্ধ সসীম মহাবিশ্বে (4/3)πr^2 ব্যাসার্ধের পরিমণ্ডলের পৃষ্ঠতলের ক্ষেত্রফল হয় 4πr^2 এর চেয়ে ছোটো এবং আয়তন হয় (4/3)πr^2-এর চেয়ে ছোটো। এই স্পেস (স্থান) কে বলা হয় গোলাকার স্পেস (স্ফেরিক্যাল স্পেস)’। মুক্তি মহাবিশ্বের বেলায় দুটি সম্ভাবনা রয়েছে। প্রথম সম্ভাবনা হল এর জ্যামিতি হবে ইউক্লেডের স্পেসের জ্যামিতির মতই। আর দ্বিতীয় সম্ভাবনায় r ব্যাসার্ধের একটি পরিমণ্ডলের পৃষ্ঠতলের ক্ষেত্রফল হয় 4πr^2-এর চেয়ে বড়ো এবং আয়তন 4πr^2-এর চেয়ে বড়ো। এই ধরনের স্পেসকে বলা হয় ‘হাইপারবোলিক স্পেস’।

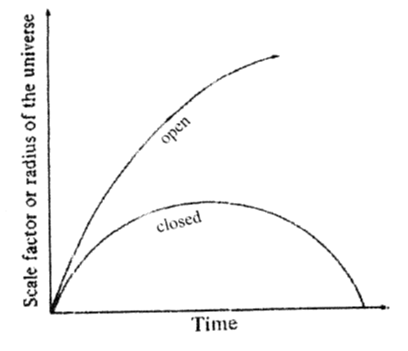
চিত্র-৫.১ : মহাবিশ্বের বস্তুর ঘনত্বের ওপর নির্ভর করে মধ্যাকর্ষণ হয়ত অবশেষে মহাবিশ্বের বর্তমান প্রসারণকে থামিয়ে দেবে। ফলে আসবে মহাবিশ্বের পতন। অথবা মহাবিশ্ব চিরকালই প্রসারিত হবে। প্রথম বিষয়টি বদ্ধ মহাবিশ্বের মডেলের সঙ্গে সম্পর্কযুক্ত আর দ্বিতীয়টি অর্থাৎ চিরকালব্যাপী প্রসারণের ব্যাপারটি মুক্ত মহাবিশ্বের মডেলের সঙ্গে সম্পর্কযুক্ত।

একটি গোলাকার পরিমণ্ডলের পৃষ্ঠদেশের ওপর, এক সিটের হাইপারবোলয়েড পৃষ্ঠদেশের ওপর এবং সমতল ভূমিতে একটি করে বৃত্ত বিবেচনা করলে আমরা এই স্থানের দ্বি-মাত্রিক এনালগ (উপমিতি)-গুলো পেতে পারি। এই বিষয়গুলো ৫.২ নম্বর চিত্রে দেখানো হল। সমতল ভূমিতে r ব্যাসার্ধের একটি বৃত্তের পরিধি ও ক্ষেত্রফল 2πr এবং πr^2। গোলীয় পৃষ্ঠদেশে r ব্যাসার্ধের একটি বৃত্তের পরিধি ও ক্ষেত্রফল যথাক্রমে 2πr এবং πr^2-এর চেয়ে ছোটো। এক্ষেত্রে বৃত্তের কেন্দ্র থেকে মহাবৃত্ত বরাবর পরিধির দিকে বৃত্তের ব্যাসার্ধকে পরিমাপ করতে হয়। আবার এক সিটের হাইপারবোলয়েড পৃষ্ঠদেশের ওপর r ব্যাসার্ধের একটি বৃত্তের পরিধি হয় 2πr এর চেয়ে বড়ো এবং ক্ষেত্রফল হয় πr^2 এর চেয়ে বড়ো। যে কোনও পৃষ্ঠতলের ক্ষেত্রে বৃত্তটিকে বক্ররেখা হিসেবে বিবেচনা করতে হয় যার ‘দূরত্ব’ একটি নির্দিষ্ট বিন্দু (কেন্দ্র) থেকে পৃষ্ঠতল বরাবর একই থাকে। এখানে, ‘দূরত্ব’ হচ্ছে পৃষ্ঠতলের ওপর অধিশায়িত বা ভূমিতিক ক্ষুদ্রতম বক্ররেখা যাকে বলা হয় ‘জিওডেসিক’ যে বিষয়টি পূর্বে উল্লেখ করা হয়েছিল। এই উপমিতিগুলো (এনালগ ) ব্যাখ্যা দেয় যে, কেন বদ্ধ মহাবিশ্বের জ্যামিতিকে স্ফেরিক্যাল (গোলীয়) বলা হয় এবং মুক্ত মহাবিশ্বের ক্ষেত্রে দুই ধরনের জ্যামিতি ইউক্লেডীয় (সমতল) এবং হাইপারবোরিক কেন। একদিক থেকে হাইপারবোলিক স্পেসের জন্য এক সিটের একটি হাইপারবোলয়েড পৃষ্ঠতল উত্তম এনালগি নয়। কারণ এখানে পূর্বেরটির কেন্দ্র আছে পরবর্তীটির নেই।

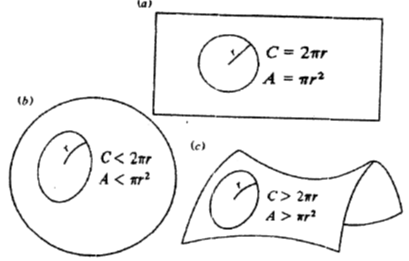
চিত্র-৫.২ : a হচ্ছে সমতল পৃষ্ঠতলের একটি উপমিতি, b হচ্ছে গোলীয় পৃষ্ঠতল এবং c তে এক সিটের হাইপারবোলয়েড (অধিবৃত্তীয়) পৃষ্ঠতল। এখানে C হচ্ছে পরিধি এবং A হচ্ছে ক্ষেত্রফল।

r ব্যাসার্ধের একটি গোলীয় পরিমণ্ডলের পৃষ্ঠতলের ক্ষেত্রফল পরিমাপ তৈরির মূলনীতিতে স্পেসের জ্যামিতি নির্ধারণ করা সম্ভব। মহাবিশ্ব মুক্ত না কি বদ্ধ তা নির্ধারণ করা সম্ভব (ফ্রিদম্যান মহাবিশ্ব অনুমান করে)। কিন্তু, এই পরিশীলনে এই ধরনের পরিমাপ করাটা পুরোপুরিভাবে বর্তমান প্রযুক্তির বাহিরে। স্পেসের জ্যামিতি স্বয়ং নিজেকে স্পেসের বৃহৎ পরিসরের বৈশিষ্ট্যে প্রকাশ করে। তুলনামূলকভাবে মহাবিশ্বের ক্ষুদ্র ক্ষুদ্র অংশ অধিষ্ঠিত করে এমন কার্যপদ্ধতি বিবেচনা করলে কোনও ফল লাভ হয় না। ‘ক্ষুদ্র’ দ্বারা এখানে ক্ষুদ্র দূরত্বসমূহ উপমিত হয় যেগুলোতে মহাবিশ্ব সমরূপে প্রতীয়মান। এমনকি যদি মহাবিশ্বের জ্যামিতি স্ফেরিক্যাল (গোলীয়) বা হাইপারবোলিক (অধিবৃত্তীয়) হয়, আমাদের গ্যালাক্সির মাপকাঠিতে এর জ্যামিতি হবে প্রায় ইউক্লেডের জ্যামিতি। এরকম মাপকাঠির ওপর ভিত্তি করে জ্যামিতি থেকে সূক্ষ্ম পথ পরিমাপ করা অত্যন্ত কঠিন। কেবল বড়ো পরিসরের মাপকাঠির অর্থাৎ আন্তঃছায়াপথীয় (ইন্টারগ্যালাটিক) দূরত্বসমূহের বৃহৎ তুলনায় জ্যামিতি তাৎপর্যপূর্ণভাবে ইউক্লেডের জ্যামিতি থেকে ভিন্ন হবে (নন-ইউক্লেডিয়ান জ্যামিতি)।

মহাবিশ্বের এরকম মডেল নেওয়া কী সম্ভব যে সব মডেলে মহাবিশ্ব চিরকালই সম্প্রসারিত হয় কিন্তু এতে স্থান হয় সসীম? আবার বিকল্প স্বরূপ এ ধরনের মডেল কি নেওয়া যায় যেগুলো ভবিষ্যতের কোনও এক সময় প্রসারণ থামিয়ে দিয়ে অবশেষে হবে বিনষ্ট কিন্তু এর স্থান হবে অসীম? যদি কেউ আইনস্টাইনের তথাকথিত ‘মহাজাগতিক শর্তাবলি স্বীকার করে নেন তবে এই উভয় সম্ভাবনাগুলোই ঘটতে পারে। আইনস্টাইন নিজেই মূলত তাঁর সমীকরণে এই মহাজাগতিক শর্ত হাজির করেছিলেন। তিনি তাঁর সমীকরণ সমাধানের মাধ্যমে একটি স্থির মহাবিশ্বকে গ্রহণ করার প্রয়াস করেছিলেন। বিজ্ঞানী হাবলের মহাবিশ্বের প্রসারণ আবিষ্কারের পূর্বে আইনস্টাইন তাঁর সমীকরণে মহাজাগতিক সমাধান খুঁজছিলেন। আইনস্টাইনের এই গভীর অনুভূতি ছিল যে, মহাবিশ্ব কোনও বড়ো ধরনের পরিবর্তনের সম্মুখীন হয়নি অর্থাৎ এটি স্থির ছিল। তাঁর মূল সমীকরণগুলো স্থায়ী কোনও সমাধান দেয়নি বলে একটি স্থায়ী সমাধান অর্জন করতে তিনি ‘মহাজাগতিক শর্ত (term)’ যুক্ত করেছিলেন। এই বিষয়টি তাঁর মূল সমীকরণের সরলতাকে কিছুটা ক্ষুণ্ণ করেছিল। পরবর্তীকালে তিনি দুঃখ প্রকাশও করেছিলেন যে, যদি তিনি তাঁর মূল সমীকরণগুলোর ওপর ভরসা রাখতেন, হয়ত মহাবিশ্বের প্রসারণের ভবিষ্যদ্বাণী করতে সক্ষম হতেন। অথবা সময়ের সঙ্গে মহাবিশ্ব বড়ো পরিসরের পরিবর্তনের সম্মুখীন হয় এ বিষয়টি ভবিষ্যদ্বাণী করতে হয়ত সক্ষম হতেন। মহাজাগতিক শর্ত একটি ‘স্থির’ সমাধান প্রকাশ করলেও মহাবিশ্বের চিরগতিশীল মডেলগুলোর দিকেও পথ প্রদর্শন করে। এসব মডেলের মধ্যে একটি চিরকালই প্রসারিত হয় কিন্তু স্থান ব্যাপ্তি দিকে সসীম এবং অন্য আরেকটি মডেল প্রসারণ থামিয়ে দিবে কিন্তু এতে স্থানের ব্যাপ্তি হবে অসীম। মহাজাগতিক শর্ত থেকে উদ্ভূত চিরগতিশীল মডেলগুলোকে জি. ল্যামেটারের নামানুসারে জি. ল্যামেটার মডেল বলা হয়। তিনিই প্রথম এই মডেলগুলোকে নিয়ে গবেষণা করেছিলেন।

আমরা কীভাবে বের করতে পারি যে, মহাবিশ্ব চিরকালই প্রসারিত হবে অথবা মহাবিশ্ব ভবিষ্যতের কোনও সময়ে প্রসারণ বন্ধ করে সংকোচিত হতে শুরু করবে? এই উত্তর খুঁজে পাওয়ার পরস্পর সম্পর্কযুক্ত কিছু পথ রয়েছে। একটি পথ হচ্ছে মহাবিশ্বের বর্তমান গড় ঘনত্বকে পরিমাপ করে একে একটি নির্দিষ্ট সংকট ঘনত্বের সঙ্গে তুলনা করা। এই বিষয়টি নিম্নরূপ : মহাবিশ্বের বিভিন্ন অংশসমূহ পরস্পরকে নিজেদের দিকে আকর্ষণ করে। তাই গ্যালাক্সিদের সরণ মন্থর হয়ে আসছে। এখন কী পরিমাণ মহাকর্ষীয় বল গ্যালাক্সির ওপর সক্রিয় হবে আর গ্যালাক্সি তার সরণকে মন্থর করবে তা নির্ভর করে গ্যালাক্সির বস্তুর ঘনত্বের ওপর। যে কোনও প্রদত্ত সময়ে ঘনত্ব যত বেশি হয়, বলের আকর্ষণ তত বেশি হয়। দেখা যায় যে, বস্তুর এই ঘনত্ব যদি নির্দিষ্ট সংকট ঘনত্বের বেশি হয় তবে অবশেষে সরণ থামিয়ে দেওয়ার জন্য আকর্ষণ বলও হবে যথেষ্ট। আর এই মহাকর্ষীয় বল সকল গ্যালাক্সিকে একত্রে কাছে টানবে। পক্ষান্তরে যদি এ ঘনত্ব সংকট ঘনত্বের নিচে থাকে তবে আকর্ষণ বল হবে অপর্যাপ্ত এবং প্রসারণ চিরকালই চলতে থাকবে। অবশ্যই মহাবিশ্বের ঘনত্বের পরিবর্তনের মত সংকট ঘনত্ব ও সময়ের সঙ্গে পরিবর্তিত হয়। উপরের কিয়ৎ স্থুল যুক্তি সঠিকভাবে প্রণীত হতে পারে এবং কেউ সংকট ঘনত্বের বর্তমান মান নিরূপণ করতে পারেন। এই মান হাবল ধ্রুবকের বর্তমান মানের ওপর নির্ভর করে। এই হাবল ধ্রুবককে পূর্বে উল্লেখ করা হয়েছে। স্মরণ করা যাক, আমাদের থেকে গ্যালাক্সিদের সরণ বেগ পেতে হলে কাউকে এই ধ্রুব সংখ্যা দ্বারা গ্যালাক্সিদের দূরত্বসমূহকে গুণ করতে হবে। এক্ষেত্রে এমন সব গ্যালাক্সিদের দূরত্বকে গুণ করতে যেসব গ্যালাক্সি আমাদের থেকে অতি দূরেও না এবং অতি নিকটেও না। প্রকৃতপক্ষে হাবল ধ্রুবকের বর্তমান মানের কিছু অনিশ্চয়তা রয়েছে। হাবল ধ্রুবকের সম্ভাব্য মান হচ্ছে প্রতি মিলিয়ন আলোকবর্ষে ১৫ কি.মি. সেকেন্ড^-১ থেকে ৩০ কিলোমিটার সেকেন্ড^-১ এর মধ্যে। অর্থাৎ যে কোনও একটি গ্যালাক্সি আমাদের থেকে ১০০ মিলিয়ন দূরে অবস্থিত হলে আমাদের থেকে এর সরণবেগ হবে ১৫০০-৩০০০ কিলোমিটার সেকেন্ড^-১। সৃষ্টিতত্ত্ববিদগণ প্রতি মেগাপারসেকে সরণ বেগের হিসেবে হাবলের ধ্রুবককে প্রকাশ করেন (মিলিয়ন পারসেক অর্থাৎ ৩.২৬ মিলিয়ন আলোকবর্ষ)। এই একক ব্যবহার করে হাবল ধ্রু বকের মান নির্ধারণ হয় ৫০ এবং ১০০ এর মধ্যে। প্রতি মিলিয়ন আলোকবর্ষে হাবল ধ্রুবকের ১৫ কি. মিটার সেকেন্ড^-১ মানের ক্ষেত্রে সংকট ঘনত্ব দাঁড়ায় প্রতি ঘন সেন্টিমিটারে (৫×১০)^৩০ গ্রাম প্রায় অথবা স্পেসের প্রতি তিন হাজার লিটারে প্রায় তিনটি হাইড্রোজেন অণু।

পৃথিবীর সমতল পৃষ্ঠ থেকে ঊর্ধ্বাভিমুখী একটি মিসাইল নিক্ষেপের বর্ণনার মাধ্যমে কেউ মোটামুটিভাবে একটি উপনিধি তৈরি করতে পারেন। যদি একটি সাইলকে যথেষ্ট বেগে উপড়ে নিক্ষেপ করা হয় তাহলে এটি নিক্ষিপ্ত হওয়ার পর সর্বক্ষণ মন্থর হতে থাকবে। কিন্তু সে যাই হোক মিসাইলটি অসীমত্বের দিকে হারিয়ে যাবে। এই অবস্থাটি মহাবিশ্বের এমন অবস্থার সঙ্গে মিলে যায় যাতে ঘনত্ব সংকট ঘনত্বের চেয়ে কম। মহাবিশ্বের এই অবস্থায় একটি সাধারণ গ্যালাক্সি ‘মুক্তিবেগ’ প্রাপ্ত হয়। পক্ষান্তরে মিসাইলটিকে অপর্যাপ্ত বেগে নিক্ষেপ করলে এটি চরম উচ্চতায় পৌঁছার পর আবার পৃথিবীতে ফিরে আসবে। মিসাইলটির পৃথিবীতে ফিরে আসা ‘মহাবিশ্বের ঘনত্ব সংকট ঘনত্বের চেয়ে বেশি’ অবস্থার সঙ্গে মিলে যায়। এই অবস্থায় গ্যালাক্সিদের সরণ ভবিষ্যতের এক সময়ে থেমে যায়। অবশেষে

মহাবিশ্বের পতন ঘটে। দেখানো যেতে পারে যে, ঘনত্ব সংকট ঘনত্বের নিচে হলে সব গ্যালাক্সি সার্বক্ষণিক মুক্তি বেগ পেয়ে থাকবে। অন্যদিকে ঘনত্ব সংকট ঘনত্বের বেশি হলে সকল গ্যালাক্সির বেগ হয়ে থাকবে মুক্তিবেগের নিচে। অবশেষে এরা সবাই বিনষ্ট হবে। সুতরাং, প্রসারণ কিংবা পতন যাই হোক না কেন তা হচ্ছে সমগ্র মহাবিশ্বের একটি বৈশিষ্ট্য।

দৃশ্যমান বস্তুর বর্তমান ঘনত্ব এবং গ্যালাক্সিদের অভ্যন্তরের বস্তুর ঘনত্ব বিভিন্ন উপায়ে আন্দাজ করা যেতে পারে। আর তা হচ্ছে সংকট ঘনত্বের ১/০৯ এবং ১/০৫ অংশের মাঝামাঝি যেখানে হাবলের ধ্রুবকের মান প্রতি আলোকবর্ষে ১৫ কি.মি. সেকেন্ড^-১ । অতএব, প্রতীয়মান হয় যে, মহাবিশ্ব মুক্ত অর্থাৎ এটি অনন্তকাল প্রসারিত হবে। কিন্তু, এটি নিশ্চিত নয় কারণ আন্তঃছায়াপথীয় (ইন্টারগ্যালাটিক স্থানে যেসব বস্তু রয়েছে তাদের উপস্থিতি এখনও শনাক্ত হয়নি। সুতরাং, বর্তমান ঘনত্বের সাব-ক্রিটিক্যাল প্রকৃতি অনিশ্চিত। তাই মহাবিশ্ব মুক্ত না কি বদ্ধ তা খুঁজে পাওয়ার পদ্ধতি এখনও ইঙ্গিতপূর্ণ তবে চূড়ান্ত নয়। নিউট্রন কণাগুলো ভারী হতে পারে এই আবিষ্কার মহাবিশ্বের ঘনত্বের পরিমাপকে সম্প্রতি আরও বেশি অনিশ্চিত করে তুলেছে। এই গুরুত্বপূর্ণ আবিষ্কারের প্রাসঙ্গিকতাও আমরা ব্যাখ্যা করব।

যেমনটি পূর্বেই উল্লেখ করা হয়েছিল, ‘মহাজাগতিক পটভূমি বিকিরণ’ ইঙ্গিত দেয় যে, অতীতে মহাবিশ্বের এমন একটি পর্যায়ে বস্তু এবং বিকিরণ সাম্যাবস্থায় ছিল। পূর্বের অধ্যায়ে উল্লিখিত ফোটন চিত্রের ক্ষেত্রে আমরা ভাবতে পারি ভিন্ন শক্তির অসংখ্য ফোটন দিয়ে সৃষ্ট বিকিরণ আধানযুক্ত কণাদের (যেমন-ইলেকট্রন, পজিট্রন এবং প্রোটন) দ্বারা প্রতিনিয়ত শোষিত ও নির্গত হয়। শক্তির নির্দিষ্ট পরিসরে ফোটন কণা আধানযুক্ত কণা দ্বারা যে কোনও প্রদত্ত মানে শোষিত ও নির্গত হয়। শক্তির নির্দিষ্ট পরিসরে ফোটন কণা আধানযুক্ত কণা দ্বারা যে কোনও প্রদত্ত মানে শোষিত ও নির্গত হয়। তাই বলা যায় তখন একটি সাম্যাবস্থা বিদ্যমান ছিল। এবার ফোটনের গড় মুক্ত সময়কে বিবেচনায় এনে অন্যভাবে বলা যায় যে, ফোটন আধানযুক্ত কণা দ্বারা শোষিত হওয়ার পূর্বে যতটুকু সময় অস্তিত্বমান থাকে অর্থাৎ এর গড়মুক্ত সময় মহাবিশ্বের বৈশিষ্ট্য প্রসারণের সময়ে তুলনায় অর্থাৎ মহাবিশ্বের যে সময়ে উল্লেখযোগ্য প্রসারণ হয়েছিল তার তুলনায় অতি সংক্ষিপ্ত। এই সাম্যাবস্থা প্রাথমিক মহাবিশ্বে সম্ভব কারণ উচ্চ তাপমাত্রার জন্য তখন ইলেকট্রন ও প্রোটন কণাগুলো মুক্ত ছিল অর্থাৎ পরমাণুদের মধ্যে এরা একত্রে বদ্ধ ছিল না। ‘বিগ-ব্যাং’ এর অল্প কয়েক শত হাজার বছর পর তাপমাত্রা ৩০০০ কেলভিনে পতিত হয়। আর তখন ইলেকট্রন, প্রোটন ও নিউট্রন কণাগুলো মিলিত হয়ে গঠন করেছিল হাইড্রোজেন ও হিলিয়াম পরমাণু। এই ঘটনার পর মহাবিশ্বে মুক্ত আধানসমূহ আর ছিল না অথবা যে কোনও হারে খুব অল্প পরিমাণ মুক্ত ছিল। তাই ফোটনগুলো আর অবিরত বিক্ষিপ্ত ছিল না। ফলে মহাবিশ্ব হয়ে গিয়েছিল স্বচ্ছ। ওই সময় থেকে বস্তু ও বিকিরণ সাম্যাবস্থা প্রাপ্ত হতে নিবৃত্ত হয়েছিল। মহাবিশ্ব প্রসারিত হওয়ার সঙ্গে সঙ্গে বিকিরণ শীতল হতে থাকে। বর্তমানে মহাবিশ্বের তাপমাত্রা ৩ কেলভিন। ইলেকট্রন, প্রোটন ও নিউট্রন কণাগুলো মিলিত হয়ে পরমাণু গঠন করার সময়কালকে বলা হয় ‘পুনর্মিলনের যুগ’। পুনর্মিলনের পর ফোটনের ‘গড় মুক্ত সময়’ মহাবিশ্বের বৈশিষ্ট্য প্রসারণের সময়ের চেয়ে অনেক বেশি দীর্ঘ হয়ে গিয়েছিল। বলা যেতে পারে যে, পুনর্মিলনের পর বস্তু এবং বিকিরণ পৃথক হয়েছিল অর্থাৎ সাম্যাবস্থায় পরস্পরের সঙ্গে যুক্ত হওয়া থেকে নিবৃত্ত হয়েছিল।

ইঙ্গিত রয়েছে যে, অতি প্রারম্ভিক মহাবিশ্বে বিকিরণ ছাড়াও অসংখ্য নিউট্রিনো ( netrinos ) এবং এন্টি নিউট্রিনো বিদ্যমান ছিল। এখানে ‘neutrinos (নিউট্রিনোস)’ শব্দটি দ্বারা তিন ধরনের সকল নিউট্রিনোকে বোঝানো হয়েছে। যেমন ইলেকট্রন নিউট্রিনো, মিউয়ন নিউট্রিনো, এবং টাউ নিউট্রিনো। এছাড়া এই শব্দটি দ্বারা এন্টি নিউট্রিনোদেরও বোঝানো হচ্ছে। ‘বিগ ব্যাং’-এর প্রথম সেকেন্ড বা তারও কিছু পর নিউট্রিনোদের গড় মুক্ত সময় ছিল অতি অল্প (মহাবিশ্বের বৈশিষ্ট্য প্রসারণের তুলনায়)। সুতরাং নিউট্রিনোরা বস্তুর সঙ্গে সাম্যাবস্থায় ছিল। বিগ ব্যাং- এর এক বা দুই সেকেন্ড পর যখন মহাবিশ্বের তাপমাত্রা প্রায় ১০^১০ কেলভিনের নিচে পতিত হয়েছিল তখন নিউট্রিনো এবং এন্টি-নিউট্রিনোদের ‘গড় মুক্ত সময়’ বৃদ্ধি পেয়েছিল। ফলে নিউট্রিনো এবং এন্টি-নিউট্রিনোরা প্রায় মুক্ত কণার ন্যায় আচরণ করতে শুরু করেছিল। এইভাবে মহাবিশ্ব নিউট্রিনোদের প্রতি স্বচ্ছ হয়েছিল আর নিউট্রিনোরা বস্তুর সঙ্গে সাম্যাবস্থা থেকে বেরিয়ে আসে। ফলে বস্তু ও নিউট্রিনোরা পৃথক হয়ে গিয়েছিল। ঠিক ফোটনদের মতই নিউট্রিনোগুলোও শীতল হয়ে গিয়েছিল। কেউ আবার যুক্তি প্রদর্শন করতে পারেন যে, নিউট্রিনোরা প্রায় ২ কেলভিন তাপমাত্রায় সমগ্র মহাবিশ্বে ছড়িয়ে পড়া উচিত। কিন্তু এটি শনাক্ত করতে বর্তমান প্রযুক্তিও বহুদূরে।

যদিও নিউট্রিনোদের শক্তি রয়েছে তবে এ যাবৎ পর্যন্ত মেনে নেওয়া হয়েছে যে, এরা ভরহীন। প্রকৃতপক্ষেই এরা ভরহীন হলে মহাবিশ্বের বর্তমান ঘনত্বে ‘পটভূমি’ নিউট্রিনোরা নেহাত তুচ্ছ পরিমাণ অবদান রাখবে। কিন্তু সম্প্রতি একটি গুরুত্বপূর্ণ ইঙ্গিত রয়েছে যে, নিউট্রিনো কণার ভর থাকতে পারে। নিউট্রিনোর এই সম্ভাব্য ভর হতে পারে ইলেকট্রন কণার ভরের চেয়ে কম। ইলেকট্রন এ যাবৎ পর্যন্ত পরিচিত সবচেয়ে হালকা ভরবিশিষ্ট কণা। বাস্তবিকই নিউট্রিনোগুলো ভরবিশিষ্ট হলে ‘পট’ নিউট্রিনোগুলো (অতি বেশি সংখ্যক হতে পারে) মহাবিশ্বের বর্তমান গড় ঘনত্বে উল্লেখযোগ্য পরিমাণে অবদান রাখবে। নিউট্রিনো কণাগুলো হয়ত ঘনত্বের পরিমাণকে সংকট ঘনত্বের থেকে বাড়িয়ে তুলবে। ফলে মহাবিশ্ব হতে পারে বদ্ধ। কিন্তু, এই বিশ্লেষণে অনেক অনিশ্চয়তা রয়েছে। প্রথমত যদি প্রকৃতপক্ষে নিউট্রিনোগুলো ভরবিশিষ্ট হয়, তবে এদের ভর সম্পর্কে বর্তমানে জানা নেই। এছাড়া তিন ধরনের নিউট্রিনো রয়েছে যারা বিভিন্ন ভরের হতে পারে। দ্বিতীয়ত, পটভূমি নিউট্রিনোদের সংখ্যা ঘনত্বের পরিমাণও যথাযথভাবে জানা নেই। তারপরও একটি মোটামুটি বিশ্লেষণ করার জন্য একটি অনুমান করে নেওয়া যেতে পারে যে, পটভূমি নিউট্রিনোদের সংখ্যা। ঘনত্বের পরিমাণ ফোটনদের সংখ্যা ঘনত্বের সমান। মহাবিশ্বে ফোটনদের সংখ্যা ঘনত্ব প্রতি ব্যারিয়নে প্রায় ১০০ মিলিয়ন থেকে ২০০০০ মিলিয়নের মধ্যে যে কোনও সংখ্যার হতে পারে। এখানে ব্যারিয়ন ফোটন কণাদের জাতিবাচক নাম। তাছাড়া প্রোটন, নিউট্রনসহ অধিক ভরবিশিষ্ট অনেক কণারও জাতিবাচক নাম। প্রতি ব্যারিয়নে ১০০০ মিলিয়ন ফোটনের একটি সংখ্যা বা অঙ্ক নির্ধারণ করা যাক। একইভাবে ধরে নেওয়া যাক মহাবিশ্বে প্রতি ব্যারিয়নে ১০০০ মিলিয়ন নিউট্রিনোও রয়েছে। যেহেতু এক ব্যারিয়নের আনুমানিক ভর ১০০০Mev, তাই এটি পরিষ্কার যে, নিউট্রিনোদের গড় ভর ১০ ev হলে বস্তুর বর্তমান ঘনত্বের তুলনায় নিউট্রিনোদের মোট ভর হবে ১০ গুণ বেশি। এখানে যেহেতু বস্তুর বর্তমান ঘনত্ব ব্যারিয়নদের দ্বারা তৈরি হয়েছে। অন্য কথায় আমাদের হিসাব যদি সঠিক হয় তবে এই ‘১০ev ভর’ দায়ী হবে এ মহাবিশ্ব ঠিক বদ্ধ হওয়ার ক্ষেত্রে। আমরা এখানে অনুমান করছি যে ব্যারিয়ন হিসেবে মহাবিশ্বের বর্তমান ঘনত্ব সংকট ঘনত্বের প্রায় ১/১০ অংশ। এই বিশ্লেষণে যেসব অনুমান তৈরি হয়েছে অবশ্যই এগুলোর মধ্যে অনেক বেশি অনিশ্চয়তা বিরাজমান। নিউট্রিনোদের একটি সংকট ঘনত্বের ক্ষেত্রে ১০ ইলেকট্রন ভোল্ট (ev) মানটি খুবই স্থূল। এখানে এই বিশ্লেষণটি খুবই গড়পড়তার। কিন্তু অদূর ভবিষ্যতে সৃষ্টিতত্ত্বের অধিক গুরুত্বপূর্ণ কোনও গবেষণা এই বিশ্লেষণকে এবং নিউট্রিনোদের ভরের পরীক্ষামূলক নির্ণয়কে যথাযথ করতে থাকবে। অতএব, সৃষ্টিতত্ত্ব সত্যিই একটি পরীক্ষামূলক বিজ্ঞানে পরিণত হয়েছে। মহাবিশ্বের গঠন তত্ত্বের ওপর গবেষণাগারে পরীক্ষা-নিরীক্ষায় প্রাপ্ত ফলাফলের গুরুতর প্রভাব থাকতে পারে।

মহাবিশ্বের প্রসারণ কী হারে কমে আসছে সেই হার পরিমাপের মূলনীতিতে বের করা সম্ভব যে, মহাবিশ্ব মুক্ত না কী বদ্ধ। প্রসারণ মন্দন পরিমাপের প্যারামিটারকে বলা হয় ডেসিলারেশন (মন্দন) প্যারামিটার। আমরা এখানে মূলত মহাবিশ্বের মডেলগুলোর সঙ্গে জড়িত। তাই এই দৃষ্টিকোণ থেকে ডেসিলারেশন প্যারামিটারের সংকট ঘনত্বের সঙ্গে সম্পর্ক রয়েছে। প্রকৃতপক্ষে উপযুক্ত এককে ডেসিলারেশন প্যারামিটার হয় সংকট ঘনত্ব ও প্রকৃত ঘনত্বের অনুপাতের অর্ধেক। ডেসিলারেশন প্যারামিটারকে পরিমাপ করতে অবশ্যই অতি দূরে গ্যালাক্সিদের এবং সংগতিপূর্ণভাবেই পূর্ববর্তী সময়সমূহের দিকে নজর দিতে হবে। এ থেকে শুরুর দিকে মহাবিশ্ব কী হারে প্রসারিত হয়েছিল তা নির্ণয় করা যাবে। আর পরবর্তী সময়গুলোতে মহাবিশ্ব কী হারে প্রসারিত হচ্ছে সে হারের সঙ্গে ওই পূর্ববর্তী হারের একটা তুলনা করা যেতে পারে। অতি দূরের গ্যালাক্সিগুলোকে তাদের দূরত্বের জন্য নিষ্প্রভ দেখাতে পারে অথবা এরা আদতই অনুজ্জ্বল অর্থাৎ তাদের পরম উজ্জ্বলতা খুবই কম। ফলে উপরোল্লিখিত পর্যবেক্ষণগুলোতে বিবেচনাযোগ্য অনিশ্চয়তা থেকে যায়। সুতরাং প্রয়োজন ‘মানবাতি (Standard Candles)’ বিবেচনা করা যাদের উজ্জ্বলতা সম্পর্কে যে কেউ নিশ্চিত হতে পারেন। কিন্তু এখানে একটি জটিলতার সৃষ্টি হয়ে যায়–হয়ত মহাবিশ্ব এবং গ্যালাক্সিদের বিবর্তন পরম উজ্জ্বলতায় প্রভাব ফেলতে পারে যার ধরন অপরিচিত।

তথাকথিত ‘গ্যালাটিক ক্যানিবালিজম (সজাতিভক্ষণ)’-এর দরুন দূরবর্তী গ্যালাক্সিদের পরম উজ্জ্বলতার ওপর প্রভাব পড়তে পারে। প্রিন্সটন বিশ্ববিদ্যালয়ের জে.পি ওসট্রিকার এবং এস. ডি. (ট্রম্যাইন দেখিয়েছিলেন যে, বৃহত্তর গ্যালাক্সিগুলো কেবল নিজেদের নক্ষত্রসমূহের বিবর্ধনের জন্যই বিবর্ধিত হয় না, কিছু গ্যালাক্সি তাদের অতি ক্ষুদ্র প্রতিবেশীদের ভক্ষণ করেও বিবর্ধিত হয়। এই প্রক্রিয়াকে বলা হয় ‘গতিশীলতার সংঘর্ষ’। এবার একটি নক্ষত্র স্তবক কল্পনা করা যাক যাতে বহুসংখ্যক নক্ষত্র রয়েছে। বিবেচনা করা যাক, স্তবকের অধিক শক্তিশালী নক্ষত্রগুলো ওই স্তবকের বাহিরের সদস্যদের সঙ্গে সংঘর্ষে জড়িয়ে পড়ে। এই সংঘর্ষের ফলে অধিকতর ভারী নক্ষত্র ধীরগতিসম্পন্ন হয়ে যায়। এক সময়ে এই সংঘর্ষ স্তবকের মধ্যাকর্ষণ শক্তিকে ধীর করে ফেলে। স্তবকটি ওই ভারী নক্ষত্রের ওপর অধিকতর প্রভাব বিস্তার করে। ফলে এই ভারী নক্ষত্রটি মধ্যাকর্ষণের দরুন স্তবকের কেন্দ্রের দিকে ঝুঁকে যায়। আর স্তবক তখন নক্ষত্রটিকে ভক্ষণ করে নেয়। একই ব্যাপার ঘটে পৃথিবীর চারদিকে ঘূর্ণমান স্যাটেলাইটের ক্ষেত্রে। স্যাটেলাইটটি কৃশ নভোমণ্ডলের ‘সান্দ্রটান’ অনুভব করে এবং ক্রমান্বয়ে ধীর গতিসম্পন্ন হয়ে যায়। স্যাটেলাইটটির গতি কমে যায় বলে তার ওপর পৃথিবীর মধ্যাকর্ষণ শক্তি অধিক বলবৎ হয়ে যায়। তাই অবশেষে স্যাটেলাইটটি নিচে নেমে আসে। এইভাবে যখন একটি ছোটো গ্যালাক্সি অধিকতর বৃহৎ গ্যালাক্সির চারপাশের একটি কক্ষপথে অবস্থান করে, দুই গ্যালাক্সির বাহিরের স্তরগুলোর মিথস্ক্রিয়তার দরুন তখন ছোটোটির গতি কমে যায় এবং অবশেষে আকর্ষণ টানের জন্য পাক খেতে খেতে অধিকতর বৃহৎ গ্যালাক্সিটির অভ্যন্তরস্থ হয় (৫.৩ নম্বর চিত্রে এই বিষয়টি দেখানো হল)। যেমনটি মূলত ধরে নেওয়া হয়েছিল যে, দূরবর্তী গ্যালাক্সিগুলোর পরম উজ্জ্বলতা কম হয়। কিন্তু এক্ষেত্রে গ্যালাটিক ক্যানিবালিজম মান বাতির পরম উজ্জ্বলতাকে প্রভাবিত করে। এতে দেখা যায় দূরের গ্যালাক্সিগুলোতে পরম উজ্জ্বলতা নিয়ে পূর্বে যা ভাবা হয়েছিল তার থেকে কম হয়ে যায়। আর এই বিষয়টি ডেসিলারেশন প্যারামিটারের পরিমাপকে প্রভাবিত করে। হয়ত কিছু বছর পূর্বে কিছুটা আত্মবিশ্বাসের মাত্রার ওপর ভিত্তি করে এই ডেসিলারেশন প্যারামিটারকে পরিমাপ করা হয়েছিল। কিন্তু এই পরিমাপে অনেক অনিশ্চয়তা রয়েছে।

মহাবিশ্ব মুক্ত না বদ্ধ তা খোঁজে বের করার জন্য অন্য একটি উপায় হচ্ছে মহাবিশ্বের ঠিকঠাক বয়স নির্ধারণ করে এই বয়সকে তথাকথিত ‘হাবলের সময়’- এর সঙ্গে তুলনা করা। ধরা যাক, মহাবিশ্বের বিভিন্ন অংশসমূহের মধ্যে পারস্পরিক মধ্যাকর্ষণ ছিল না। এক্ষেত্রে অতীত সময়ে বস্তুর সরণ বেগ এবং বর্তমান সময়ের সরণ বেগ একই হবে।

সহজেই দেখানো যেতে পারে যে, গ্যালাক্সিগুলোর পরস্পরে সঙ্গে সংকুচিত অবস্থায় ছিল। আর অতীতের এক সময়ে ‘বিগ ব্যাং’ অর্থাৎ মহাবিশ্বের সৃষ্টি হয়েছিল। এই সময়কে বলা হয় হাবলের সময়। আর হাবল ধ্রুবকের উপযুক্ত একক সমূহের পূরক দিয়ে এই সময় নির্ধারণ করা যায়। হাবল ধ্রুবকের ১৫ কিলোমিটার সেকেন্ড^-১ মিলিয়ন^-১ মানের জন্য হাবলের সময় হবে ২০ বিলিয়ন বছর। অর্থাৎ প্রায় ২০ বিলিয়ন বছর পূর্বে ‘বিগ ব্যাং’ সৃষ্টি হয়েছিল। মুক্ত মহাবিশ্বের চেয়ে বদ্ধ মহাবিশ্বে প্রসারণের হার খুব দ্রুত কমছে।

সুতরাং, ‘বিগ ব্যাং’ থেকে এখনও পর্যন্ত যে সময় অতিক্রান্ত হয়েছে সেই অতিক্রান্ত সময়ের পরিমাণ বদ্ধ মহাবিশ্বের বেলায় তুলনামূলক কম হবে। অর্থাৎ মুক্ত মহাবিশ্বের চেয়ে বদ্ধ মহাবিশ্বে এখনও পর্যন্ত কম সময় অতিক্রান্ত হয়েছে। কেউ দেখাতে পারেন যে, মহাবিশ্বের বয়স হাবলের সময়ের চেয়ে ২/৩ অংশ কম হলে মহাবিশ্ব হবে বদ্ধ। অন্যদিকে মহাবিশ্বের বয়স হাবলের সময় থেকে ২/৩ অংশ বেশি হলে মহাবিশ্ব হবে একটি মুক্ত মহাবিশ্ব। যাই হোক, মহাবিশ্বের বয়স এবং হাবলের সময় এই উভয় ক্ষেত্রেই অনিশ্চয়তা রয়েছে। বর্তমান পর্যবেক্ষণে অনিশ্চয়তাগুলো এতই প্রকট যে, এই বিশেষ অভিগমন থেকে নির্দিষ্ট একটি সিদ্ধান্তে যাওয়া একেবারেই অসম্ভব।

চিত্র-৫.৩ : একটি বৃহৎ গ্যালাক্সি তার একটি ছোটো প্রতিবেশীকে ভক্ষণ করতে পারে।

মহাবিশ্বের বস্তুসমূহের অধিকাংশই হাইড্রোজেন ও হিলিয়ামের রূপ। একটি হাইড্রোজেন পরমাণুতে একটি প্রোটন ও একটি ইলেকট্রন রয়েছে। আর হিলিয়াম পরমাণুর কেন্দ্রীণে আছে দুটি প্রোটন ও দুটি নিউট্রন এবং পরমাণুর কেন্দ্রীণের চারপাশে আছে দুটি ইলেকট্রন। হাইড্রোজেন মহাবিশ্বের প্রায় ৭০ থেকে ৮০ শতাংশ বস্তু (মোট ভর বিবেচনায়) বস্তু অংশীভূত করে রেখেছে। অন্যদিকে হিলিয়ামে অন্তর্ভুক্ত আছে প্রায় ২০ থেকে ৩০ শতাংশ বস্তু। শতকরা হারে মোট বস্তুর অল্প পরিমাণ অন্যান্য উপাদানগুলোতে অন্তর্ভুক্ত। হাইড্রোজেন ও হিলিয়াম সবচেয়ে হালকা। বিশ্বাস করা হয় যে, যেসব পদার্থ সংশ্লেষিত হয়েছে তাদের মধ্যে হাইড্রোজেন হচ্ছে আদিম। হাইড্রোজেন কেন্দ্রীণ তথা প্রোটন থেকে ভারী কেন্দ্ৰীণ প্রস্তুত করতে উচ্চ তাপমাত্রার প্রয়োজন। উচ্চ তাপমাত্রায় বিটা ভাঙনের বিপরীত প্রক্রিয়ায় ইলেকট্রনের উপস্থিতিতে কিছু সংখ্যক প্রোটন নিউট্রনে পরিণত হয়। অর্থাৎ একটি প্রোটন ও একটি ইলেকট্রন মিলিত হয়ে একটি নিউট্রন ও একটি নিউট্রিনো তৈরি করে। উচ্চ তাপমাত্রায় প্রোটন ও নিউট্রনদের মধ্যে একটি সাম্যাবস্থা বিরাজ করে আর নিউট্রনের অনুপাত তাপমাত্রার ওপর নির্ভর করে। অতীতে মহাবিশ্বে তিনটি অবস্থায় অতি উচ্চ তাপমাত্রা বিরাজমান ছিল প্রথমত, বিগ ব্যাং-এর প্রথম কিছু মিনিট, দ্বিতীয়ত উত্তপ্ত নক্ষত্রের কেন্দ্রে এবং তৃতীয়ত সুপার নোভা বিস্ফোরণে পরবর্তী অধ্যায়ে সুপার নোভার বর্ণনা করা হবে। প্রোটন ও নিউট্রন থেকে হিলিয়াম কেন্দ্ৰীণ সৃষ্টি হওয়ার সময়ে নির্দিষ্ট পরিমাণ শক্তি বিমুক্ত হয়। মহাবিশ্বে হাইড্রোজেন থেকে হিলিয়ামে বস্তুর ২০ থেকে ৩০ শতাংশ রূপান্তরে যে পরিমাণ শক্তি বিচ্ছুরিত হয় তা মহাবিশ্বের সকল নক্ষত্র দ্বারা বিচ্ছুরিত মোট শক্তির পরিমাণের চেয়ে (বিগ ব্যাংগ) এর কয়েক মিনিট পর নক্ষত্র সৃষ্টির সময় থেকে) বেশি। এই বিষয়টি কাউকে বিশ্বাস করাতে বাধ্য করে যে, হিলিয়াম নক্ষত্রের মধ্যে সংশ্লেষিত হওয়ার পূর্বে মহাবিশ্বের পূর্ববর্তী পর্যায়গুলোতে সংশ্লেষিত হয়েছিল। ভারী উপাদানসমূহের বিবেচনায় ই.ই. স্যালপিটার ও ই.এম. বারজি, জি.এফ বারবিজ এবং এফ. হোয়েল দেখিয়েছিলেন যে, উষ্ণ নক্ষত্রদের কেন্দ্রে এবং সুপারনোভা বিস্ফোরণের মধ্যে অধিকাংশ ভারী উপাদানগুলো দগ্ধিভূত হওয়া খুবই সম্ভব। এই ‘দগ্ধিকরণ’ প্রক্রিয়াকে বলা হয় ‘কেন্দ্রীণ সংশ্লেষ’। কিন্তু মহাবিশ্বের গোড়ার দিকে হিলিয়াম সংশ্লেষণ সম্ভব ছিল, কিন্তু অধিকতর ভারী উপাদান উৎপন্ন হওয়া কিছুটা কঠিন ব্যাপারই ছিল। কারণ প্রাথমিক মহাবিশ্বে পটভূমি বিকিরণের তাপমাত্রা অতি বেশি হওয়ার কথা। তখন এই বিকিরণ তীক্ষ্ণতা হয়ত ভারী কেন্দ্রীণ সৃষ্টি হওয়া মাত্রই সেই কেন্দ্রীণকে ভেঙে দিতো। বর্তমানে মহাবিশ্বে অধিক পরিমাণে হাইড্রোজেনের উপস্থিতি থেকে কেউ মহাবিশ্বের প্রথম কয়েক মিনিটের তীব্র বিকিরণের একটি ধারণায় উপনীত হতে পারেন। আর এই তীব্র বিকিরণের দরুন অধিকাংশ হাইড্রোজেন ভারী উপাদানে রূপান্তরিত হতে পারেনি। মহাবিশ্বের প্রথম কয়েক মিনিটের এই তীব্র বিকিরণের উপস্থিতি থেকে বর্তমান মহাবিশ্বে পটভূমি বিকিরণের উপস্থিতি অনুমান করা যেতে পারে। এই যুক্তির প্রবাহ থেকে কেউ ‘মহাজাগতিক পটভূমি বিকিরণ’ প্রত্যাশা করতে পারেন। পেনজিয়াস ও উইলসন ১৯৬৫ সালে ‘মহাজাগতিক পটভূমি বিকিরণ’ আবিষ্কার করেছিলেন। এই আবিষ্কারের প্রায় একই সঙ্গে পি. জে. ই পিবল্স এবং তাঁর সহকর্মীগণ প্রিন্সটন বিশ্ববিদ্যালয়ে এইসব হিসাবনিকাশ সম্পন্ন করেছিলেন। মূলত তার অনেক পূর্বে অর্থাৎ বিংশ শতাব্দীর চল্লিশের দশকের শেষের দিকে জি গ্যামাউ এবং তাঁর সহকর্মীগণ ৫ কেলভিন তাপমাত্রা বিশিষ্ট পটভূমি বিকিরণের ভবিষ্যদ্‌বাণী করেছিলেন। তাঁদের এই কাজ বহুল পরিমাণে উপেক্ষিত হয়েছিল। এই উপেক্ষার আংশিক কারণ ছিল ‘কেন্দ্রীণ সংশ্লেষণের তত্ত্ব’ যার ওপরই ভিত্তি ছিল এই ভবিষ্যদ্বাণীর তা কিছু ক্ষেত্রে ভ্রান্ত প্রমাণিত হয়েছিল।

গোড়ার দিকে মহাবিশ্বে হিলিয়াম সংশ্লেষণের পূর্বে প্রোটন ও নিউট্রন কণাগুলো মিলিত হয়ে ডিউটেরিয়াম কেন্দ্রীণ সৃষ্টি করেছিল। এই ডিউটেরিয়াম কেন্দ্রীণ একটি প্রোটন ও একটি নিউট্রনের সমন্বয়ে সৃষ্টি (ডিউটেরিয়াম হচ্ছে বারী পানির (HDO) উপাদান)। ট্রিটিয়াম ও হিলিয়াম-৩ এর মধ্যবর্তী ধাপের মাধ্যমে ডিউটেরিয়াম কেন্দ্রীণটি হিলিয়ামে সংশ্লেষিত হয়েছিল। উল্লেখ্য, ট্রিটিয়াম একটি প্রোটন ও দুটি নিউট্রন দ্বারা গঠিত এবং হিলিয়াম থ্রি দুটি প্রোটন এবং একটি নিউট্রন দ্বারা গঠিত। কিন্তু ডিউটেরিয়ামের অস্থায়িত্বের কারণে নক্ষত্রের মধ্যে ডিউটেরিয়াম সৃষ্টি হওয়া খুবই কঠিন। তাই মহাবিশ্বে ডিউটেরিয়ামের অধিকাংশই আগেই সৃষ্টি হয়েছিল অর্থাৎ মহাবিশ্বের প্রথম কয়েক মিনিটে এরা সংশ্লেষিত হয়েছিল। এবার মহাবিশ্ব বদ্ধ হলে তার বর্তমান ঘনত্ব অপেক্ষাকৃত বেশি হবে (এই ঘনত্ব সংকট ঘনত্বের চেয়ে বেশি)। যদি পরিস্থিতি এই হয় তবে মহাবিশ্বের যে দশায় কেন্দ্রীণ সংশ্লেষণ ঘটেছিল সেই দশায় অবশ্যই প্রোটন ও নিউট্রনসমূহের ঘনত্ব বেশি হওয়ার কথা। সুতরাং, বেশি ঘনত্বের অবস্থায় সৃষ্ট ডিউটেরিয়াম হিলিয়ামে রূপান্তরিত হয়ে থাকবে। আর অধিকতর ঘনত্বপূর্ণ অবস্থায় ডিউটেরিয়ামের রূপান্তর অপেক্ষাকৃত বেশি হয়েছিল। সুতরাং, মহাবিশ্ব যদি বদ্ধ হয় তবে কেউ বর্তমানে ডিউটেরিয়ামের অল্প প্রাচুর্য আশা করতে পারেন। অতএব, এই মূলনীতিতে ডিউটেরিয়ামের বর্তমান প্রাচুর্যতাকে সঠিকভাবে পরিমাপ করে তাকে সংকট ঘনত্বের সঙ্গে তুলনা করে আমরা একটা সিদ্ধান্ত নিতে পারি যে, মহাবিশ্ব ‘মুক্ত’ না কি ‘বদ্ধ’।

যদিও উপরের সকল বিশ্লেষণে বিবেচনাযোগ্য অনিশ্চয়তা রয়েছে, তারপরও অনেক ইঙ্গিত রয়েছে যে, আমাদের মহাবিশ্ব মুক্ত। এই স্বীকৃতিদান খুবই যথাযথ পর্যবেক্ষণ এবং সর্বোত্তম তত্ত্বের প্রতীক্ষা করে।